一.堆是什么？ 二.堆的簡單接口如何實現？ 三.堆的意義？

//////

成都創新互聯是一家集網站建設,景德鎮企業網站建設,景德鎮品牌網站建設,網站定制,景德鎮網站建設報價,網絡營銷,網絡優化,景德鎮網站推廣為一體的創新建站企業，幫助傳統企業提升企業形象加強企業競爭力。可充分滿足這一群體相比中小企業更為豐富、高端、多元的互聯網需求。同時我們時刻保持專業、時尚、前沿，時刻以成就客戶成長自我，堅持不斷學習、思考、沉淀、凈化自己，讓我們為更多的企業打造出實用型網站。1.堆是什么？

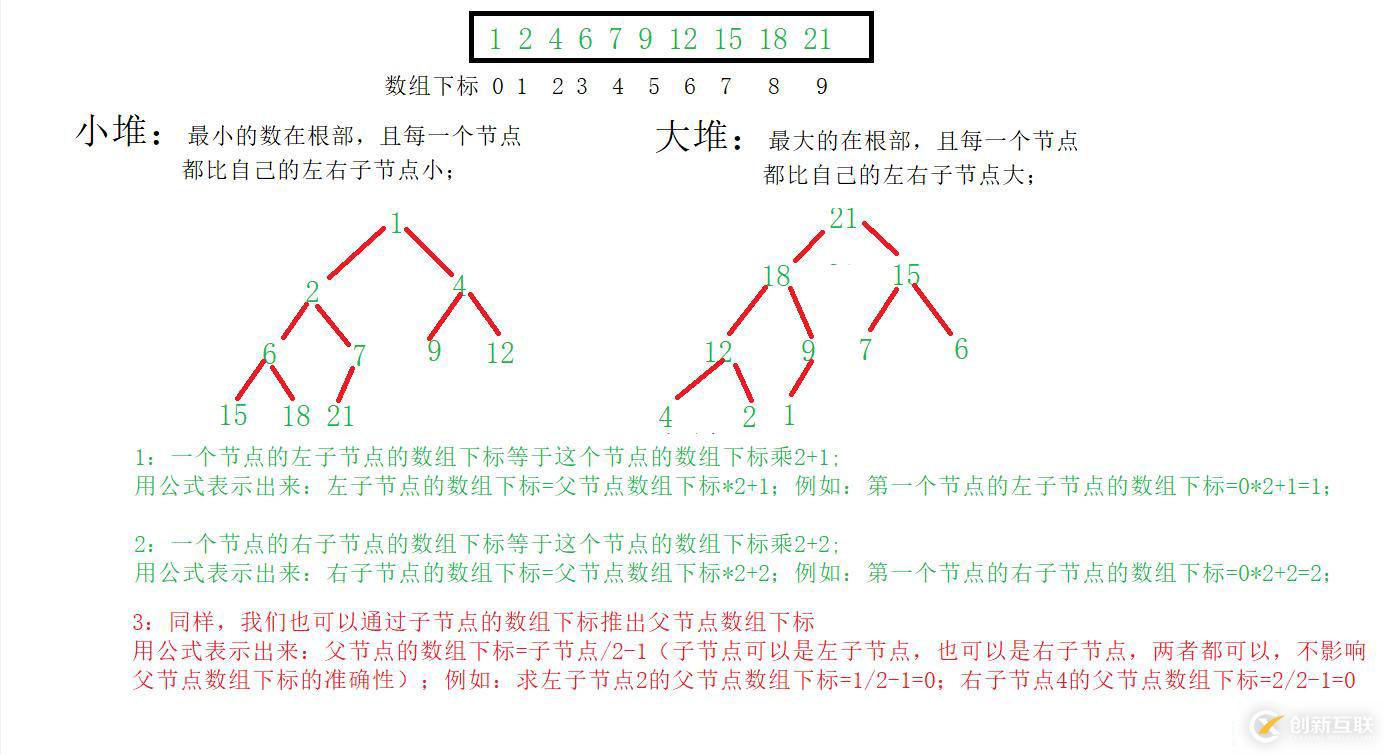
含義：堆實質上是用一維數組（比鏈表實現更優）存貯一種特殊的二叉樹（完全二叉樹）的一種順序存貯方式；所以，堆總是一顆完全二叉樹，而且堆還有大小堆之分；

大堆：根節點是堆中大的數，且每一個父節點總是大于等于自己的子節點；

小堆：根節點是堆中最小的數，且每一個父節點總是小于自己的子節點

如下圖所示：（不一定是有序的數組，這只是方便舉例）

/////

2.堆的簡單接口實現

2.1 初始化堆：既然是用一維數組實現，根據之前對棧等線性表用數組實現的學習，我們應該知道此時需要用結構體來構建其結構，結構體中包含 存貯完全二叉樹中的節點信息的數組array，記錄多少個節點的size， 以及用來判斷是否需要擴容的capacity;，具體代碼如下所示：

//定義結構體，表示堆的信息：
typedef int typedata;
typedef struct HeapNode
{
	typedata* arr;
	int size;
	int capacity;
}HP;




//初始化堆
void HeapInit(HP* ps)//這里我沒有先malloc空間，到后面插入的時候直接realloc就可以了；
{
	assert(ps);
	ps->arr = NULL;
	ps->size = ps->capacity = 0;
}

//

2.2 向堆中依次插入元素（向上調整法）：

//向堆中插入：
void swap(typedata* p1, typedata* p2)
{
	int temp = *p1;
	*p1 = *p2;
	*p2 = temp;
}
void AdjustUP(typedata* ps, int child)
{
	int parent = (child - 1) / 2;//找到此時子節點的父節點，比較看是否需要向上調整；
	while (child >0)
	{
		if (ps[child] >ps[parent])//如果子節點的值大于父節點的值
		{
			swap(&ps[child], &ps[parent]);//交換函數：交換子節點與父節點的值；
			child = parent;//將父節點的數組下標給子節點，
			parent = (child - 1) / 2;//讓子節點找到新的父節點，繼續比較；
		}
		else
		{
			break;
		}
	}
}
void HeapPush(HP* ps, typedata x)
{
	assert(ps);

	//擴容:
	if (ps->size == ps->capacity)
	{
		ps->capacity = 0 ? 4 : ps->capacity * 2;
		typedata* ptr = realloc(ps->arr,sizeof(typedata) *(ps->capacity));
		if (ptr == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		ps->arr = ptr;
	}
	ps->arr[ps->size] = x;
	ps->size++;

	//向上調整建堆：
	AdjustUP(ps->arr, ps->size - 1);
}



//定義數組，調用插入接口依次插入：
int arr[10] = { 17,11,12,25,36,46,71,42,29,100 };
for (int i = 0; i< sizeof(arr) / sizeof(arr[0]); i++)
{
	//向堆中依次插入元素：
	HeapPush(&ps, arr[i]);
}

//

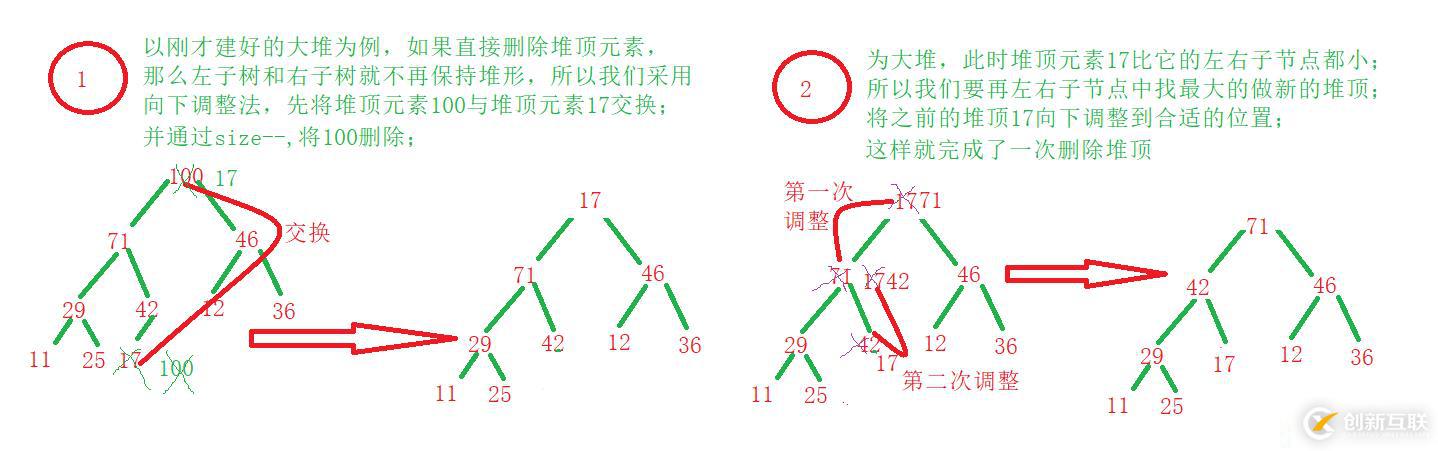
2.3 刪除堆頂元素（向下調整法）：

void AdjustDown(typedata* ps, int n, int parent)
{
	assert(ps);
	int child = parent * 2 + 1;
	while (childps[parent])
		{
			swap(&ps[parent], &ps[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
//刪除堆頂元素接口：
void HeapPop(HP* ps)
{
	assert(!HeapEmpty(ps));
	swap(&ps->arr[0], &ps->arr[ps->size - 1]);//先將堆頂與堆底交換；
	ps->size--;//利用數組下標刪除掉交換過來的堆頂；

	//向下調整建堆：
	AdjustDown(ps->arr, ps->size - 1, 0);

	
}

//

2.4 Topk問題（取堆中k個大或最小的元素）：

//Top(選取大或最小的元素)接口:
typedata HeapTop(HP* ps)//有返回值；
{
	assert(!HeapEmpty(ps));//調用判空接口對結構體判空
	return ps->arr[0];//返回堆頂元素；
}	


//Topk問題：取堆中大或最小的前K個元素：
int k = 5;
while(k--)
{
	printf("%d ", HeapTop(&ps));//調用Top接口，獲取堆頂元素，并打印出來；
	HeapPop(&ps);//調用刪除堆頂元素接口，刪除掉打印過的堆頂，找堆中新的堆頂，實現多次尋找；
}

//

2.4 堆中元素個數，判空，打印以及銷毀：

這幾個接口比較簡單，直接給出代碼：

//判空：
bool HeapEmpty(HP* ps)
{
	assert(ps);
	return ps->size == 0;
}

//堆中元素個數：
size_t Heapsize(HP* ps)
{
	assert(!HeapEmpty(ps));
	return ps->size;
}

//打印堆：
void HeapPrint(HP* ps)
{
	assert(!HeapEmpty(ps));
	int i = 0;
	for (i = 0; i< ps->size; i++)
	{
		printf("%d ", ps->arr[i]);
	}
	printf("\n");
}

//銷毀堆：
void HeapDestroty(HP* ps)
{
	assert(ps);
	free(ps->arr);
	ps->arr = NULL;
	ps->size = ps->capacity = 0;
}

/////

3，堆的意義？

意義：堆的意義在于存貯完全二叉樹時同時可以通過堆排序（時間復雜度為O(n*log N)），快速的進行排序，此意義我將會在后面與其他幾種排序中盡我大的能力去說明與理解；

/////

至此，這是我對堆的創建，堆的一些簡單接口的實現的全部理解，如有不足之處，請各位大佬不吝賜教，謝謝！

你是否還在尋找穩定的海外服務器提供商？創新互聯www.cdcxhl.cn海外機房具備T級流量清洗系統配攻擊溯源，準確流量調度確保服務器高可用性，企業級服務器適合批量采購，新人活動首月15元起，快前往官網查看詳情吧

分享標題：C語言實現堆的一些簡單接口-創新互聯
網頁網址：http://vcdvsql.cn/article12/dchddc.html

成都網站建設公司_創新互聯，為您提供自適應網站、營銷型網站建設、企業建站、品牌網站建設、動態網站、Google

廣告

聲明：本網站發布的內容（圖片、視頻和文字）以用戶投稿、用戶轉載內容為主，如果涉及侵權請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網站立場，如需處理請聯系客服。電話：028-86922220；郵箱：631063699@qq.com。內容未經允許不得轉載，或轉載時需注明來源： 創新互聯