什么是堆

堆是一種叫做完全二叉樹的數據結構，可以分為大根堆，小根堆，而堆排序就是基于這種結構而產生的一種程序算法。

創新互聯建站主營涇川網站建設的網絡公司,主營網站建設方案,重慶APP軟件開發,涇川h5成都小程序開發搭建,涇川網站營銷推廣歡迎涇川等地區企業咨詢堆的分類

大根堆:每個節點的值都大于或者等于他的左右孩子節點的值

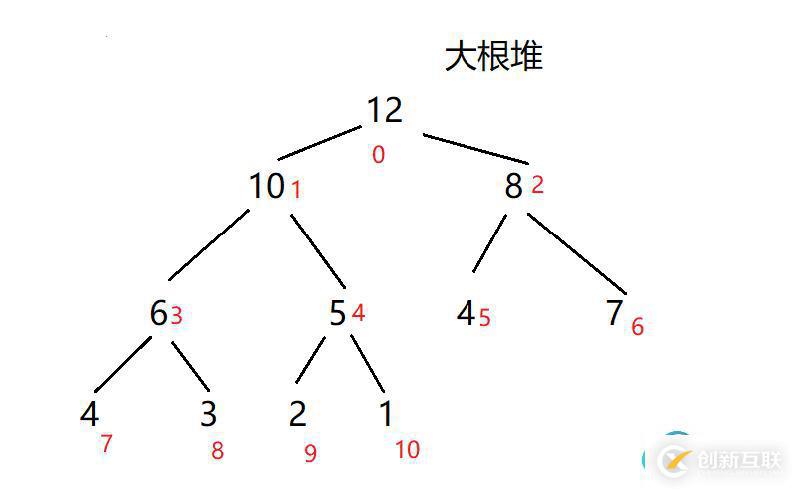
小根堆:每個結點的值都小于或等于其左孩子和右孩子結點的值

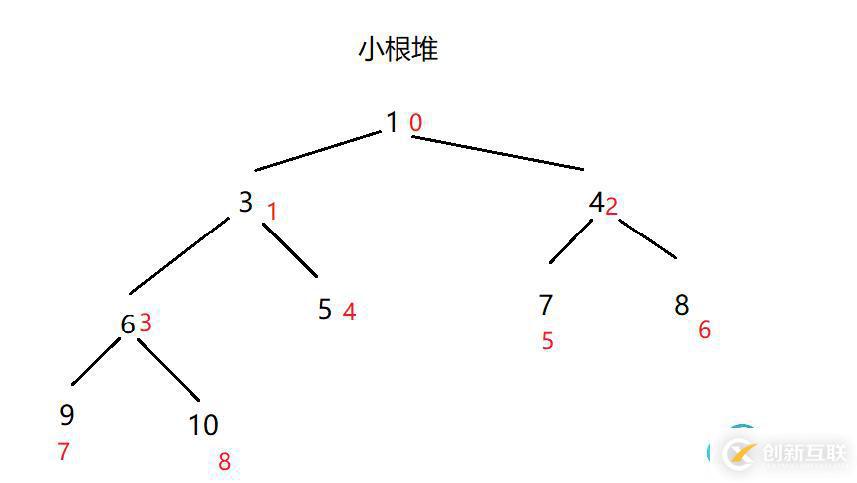
兩種結構映射到數組為:

大根堆:

小根堆:

//父-->子:i--->左孩子:2*i+1, 右孩子:2*i+2;
//子-->父:i--->(i-1)/2;?(i為下標元素)

排序思想

1.首先將待排序的數組構造成一個大根堆，此時，整個數組的大值就是堆結構的頂端

2.將頂端的數與末尾的數交換，此時，末尾的數為大值，剩余待排序數組個數為n-1

3.將剩余的n-1個數再構造成大根堆，再將頂端數與n-1位置的數交換，如此反復執行，便能得到有序數組

注意:升序用大根堆，降序就用小根堆(默認為升序)

構造堆

那么如何構造大根堆呢?

首先我們給定一個無序的序列，將其看做一個堆結構，一個沒有規則的二叉樹，將序列里的值按照從上往下，從左到右依次填充到二叉樹中。

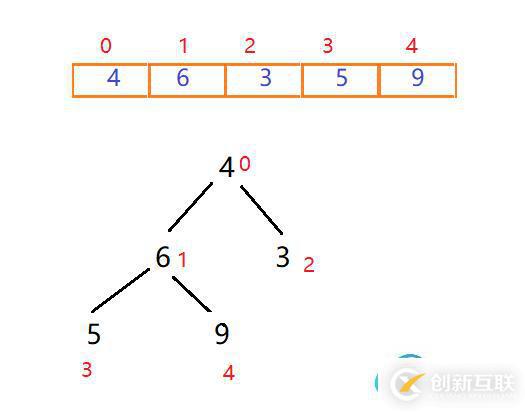
對于一個完全二叉樹，在填滿的情況下（非葉子節點都有兩個子節點），每一層的元素個數是上一層的二倍，根節點數量是1，所以最后一層的節點數量，一定是之前所有層節點總數+1，所以，我們能找到最后一層的第一個節點的索引，即節點總數/2（根節點索引為0），這也就是第一個葉子節點，所以第一個非葉子節點的索引就是第一個葉子結點的索引-1。那么對于填不滿的二叉樹呢？這個計算方式仍然適用，當我們從上往下，從左往右填充二叉樹的過程中，第一個葉子節點，一定是序列長度/2，所以第最后一個非葉子節點的索引就是 arr.len / 2 -1，對于此圖數組長度為5，最后一個非葉子節點為5/2-1=1，即為6這個節點

那么如何構建呢？ 我們找到了最后一個非葉子節點，即元素值為6的節點，比較它的左右節點中大的一個的值，是否比他大，如果大就交換位置。

在這里5小于6,而9大于6，則交換6和9的位置

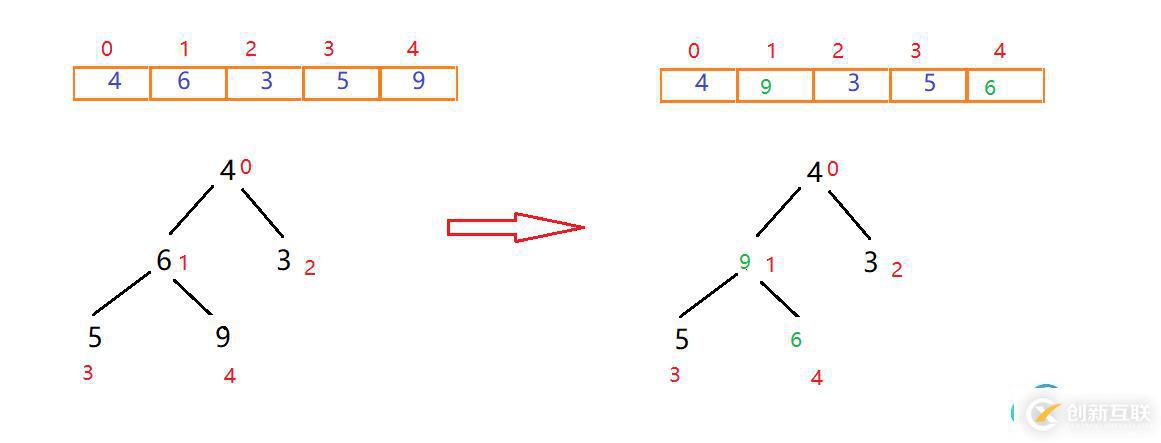
找到下一個非葉子節點4，用它和它的左右子節點進行比較，4大于3，而4小于9，交換4和9位置

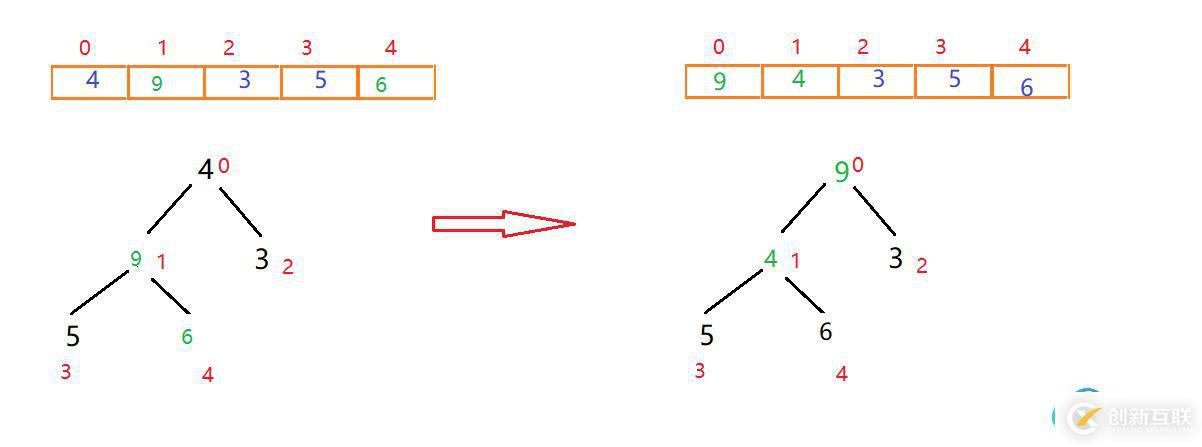
此時發現4小于5和6這兩個子節點，我們需要進行調整，左右節點5和6中，6大于5且6大于父節點4，因此交換4和6的位置

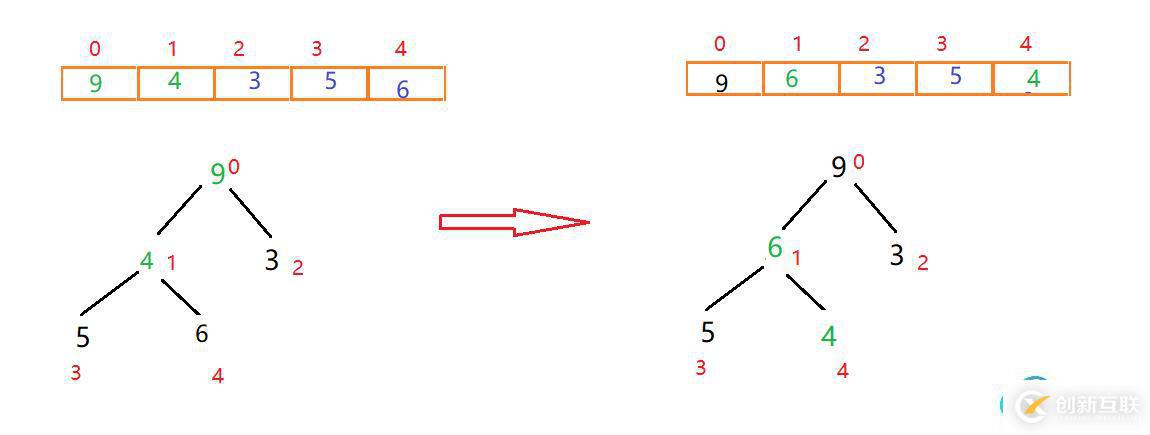
此時我們就構造出來一個大根堆,下來進行排序

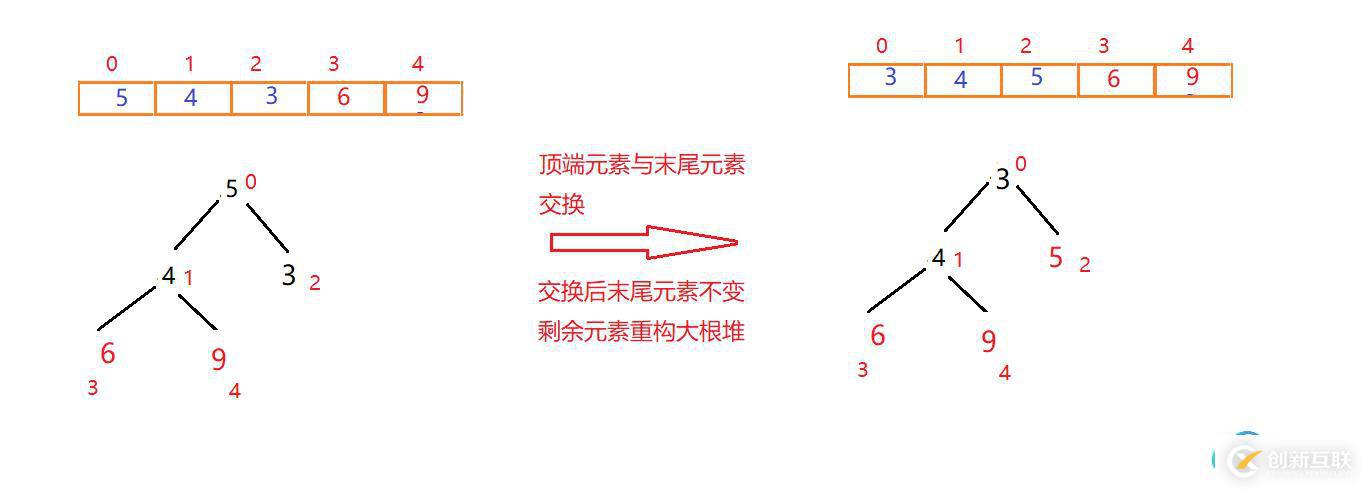
首先將頂點元素9與末尾元素4交換位置，此時末尾數字為大值。排除已經確定的大元素，將剩下元素重新構建大根堆

一次交換重構如圖: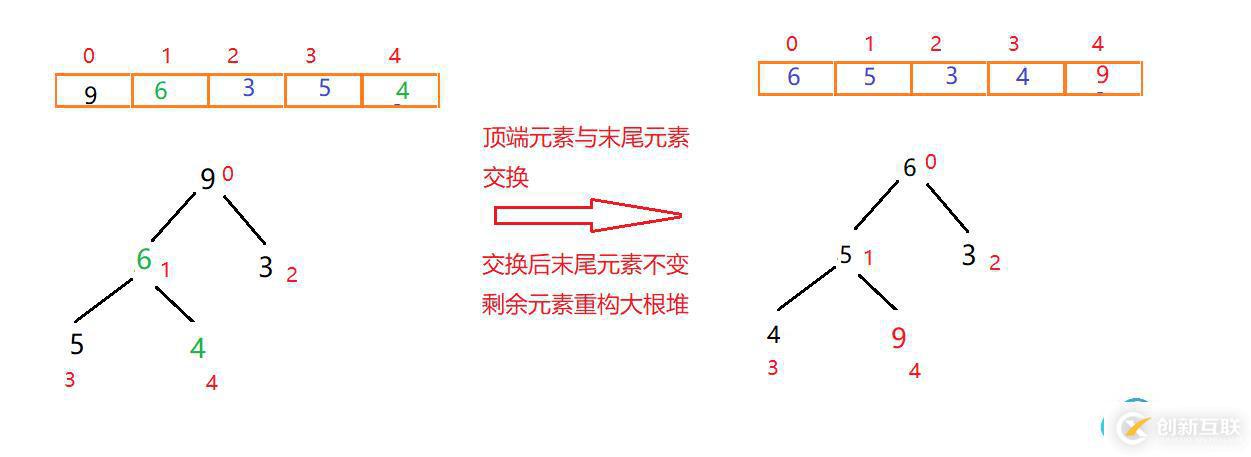

此時元素9已經有序，末尾元素則為4(每調整一次，調整后的尾部元素在下次調整重構時都不能動)

二次交換重構如圖:

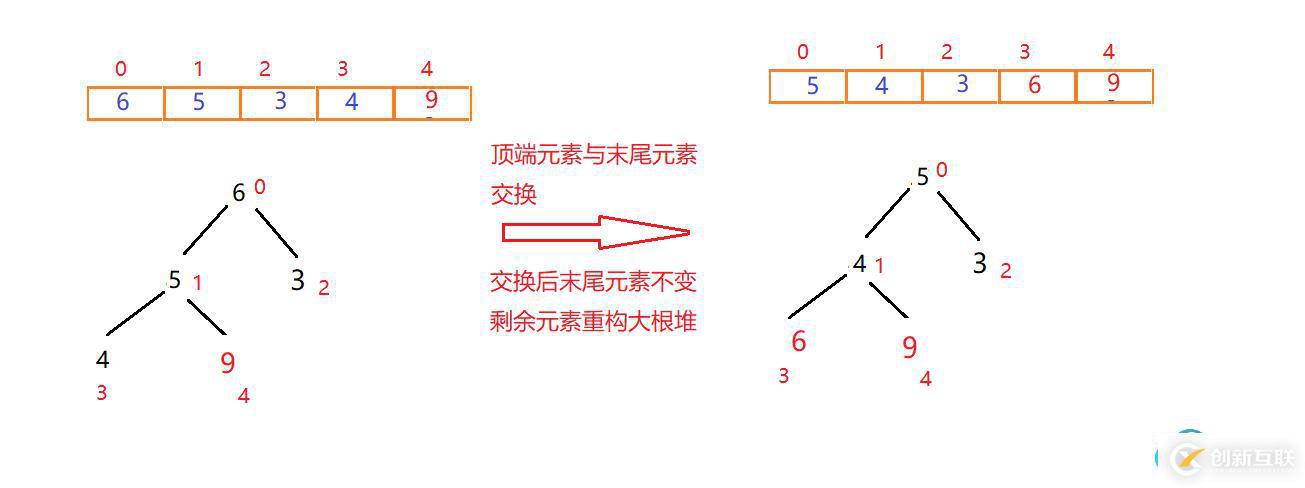
最終排序結果:?

由此，我們可以歸納出堆排序算法的步驟：

1. 把無序數組構建成二叉堆。

2. 循環刪除堆頂元素，移到集合尾部，調節堆產生新的堆頂。

當我們刪除一個大堆的堆頂（并不是完全刪除，而是替換到最后面），經過自我調節，第二大的元素就會被交換上來，成為大堆的新堆頂。

正如上圖所示，當我們刪除值為9的堆頂節點，經過調節，值為6的新節點就會頂替上來；當我們刪除值為6的堆頂節點，經過調節，值為5的新節點就會頂替上來.......

由于二叉堆的這個特性，我們每一次刪除舊堆頂，調整后的新堆頂都是大小僅次于舊堆頂的節點。那么我們只要反復刪除堆頂，反復調節二叉堆，所得到的集合就成為了一個有序集合，

堆排序是不穩定的排序，空間復雜度為O(1),平均的時間復雜度為O(nlogn),最壞情況下也穩定在O(nlogn)?

代碼示例:

void HeapAdjust(int* arr, int start, int end)
{
	int tmp = arr[start];
	for (int i = 2 * start + 1; i<= end; i = i * 2 + 1)
	{
		if (i< end&& arr[i]< arr[i + 1])//有右孩子并且左孩子小于右孩子
		{
			i++;
		}//i一定是左右孩子的大值
		if (arr[i] >tmp)
		{
			arr[start] = arr[i];
			start = i;
		}
		else
		{
			break;
		}
	}
	arr[start] = tmp;
}
void HeapSort(int* arr, int len)
{
	//第一次建立大根堆，從后往前依次調整
	for(int i=(len-1-1)/2;i>=0;i--)
	{
		HeapAdjust(arr, i, len - 1);
	}
	//每次將根和待排序的最后一次交換，然后在調整
	int tmp;
	for (int i = 0; i< len - 1; i++)
	{
		tmp = arr[0];
		arr[0] = arr[len - 1-i];
		arr[len - 1 - i] = tmp;
		HeapAdjust(arr, 0, len - 1-i- 1);
	}
}
int main()
{
	int arr[] = { 9,5,6,3,5,3,1,0,96,66 };
	HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
	printf("排序后為:");
	for (int i = 0; i< sizeof(arr) / sizeof(arr[0]); i++)
	{
		printf("%d ", arr[i]);
	}
	return 0;
}

排序結果:

路過有幫助麻煩點個贊再走！博主畫圖不容易┭┮﹏┭┮

2022/11/19 補充

這篇文章寫的也挺早的了，今天抽空重新補充一下，因為很多朋友私信我說是沒看懂或者怎么樣的，(寫的早，文筆表達確實有限)。我今天就再拿文字和簡單的圖把思路說一下，補充的我按照構建小頂堆，就是從大到小排序一組數字。也有很多朋友問啊大根堆構建出來堆頂是大的元素，你最后排序輸出可又是從小到大，問出這些問題就說明你沒有好好看步驟。

再提一嘴，像數據結構優先隊列這種他底層就是按照大根堆的方式去實現的，自動排序取出優先級最高的(默認是元素最小)，也就是從小到大排

補充：

理解堆排序，他其實就是對于一組數去進行排序(這里放在數組里)，而我們所說的大根堆，小根堆都是邏輯上的讓我們去理解排序算法，千萬別混為一談迷糊了

還是這么一組無序的數字，我們把它邏輯構造成一個完全二叉樹

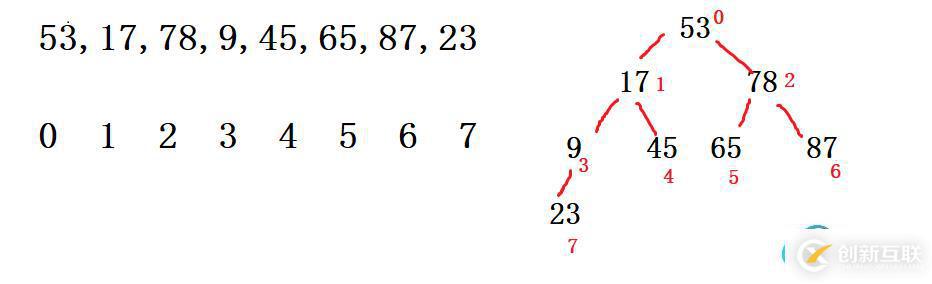
我們這里按照從大到小排序，構建小根堆的大致思路來說

我們堆排序的步驟就是這樣

先把這個最初的堆去?給他構建成一個小根堆，所謂小根堆就是堆頂元素最小

注意構建的時候就需要我們找分支結點，我最上面提到的那數學公式，我們從這個分支結點開始把它的父結點這么一個小樹弄成小根堆，再往上跳，從他的父結點開始，找雙親把他們這一部分調整成最小堆。依次類推，說白了就是從下面局部構成小根堆，一點一點，最后整體全局構建小頂堆。這樣構建之后你全局的堆頂才是最小的一個元素，這才是所謂的完整的一次構建。體現在數組上就是你數組首元素現在是最小的，因為你堆頂就代表著0號下標元素不是。（大根堆就是上面元素是大的而已，怎么構建還都是一樣啊，就是把大元素往上覆蓋，判斷條件變了而已）

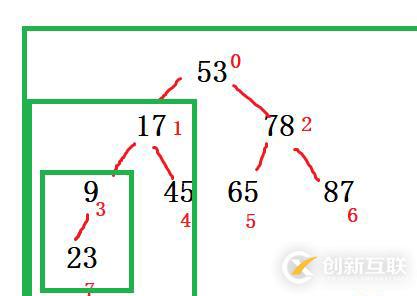
現在你首元素最小了，說明邏輯上就是個小根堆了，你是怎么倒敘呢？不就是首元素和尾元素交換。然后你數組最后面不就成了最小的（這是體現在數組上的），那么同樣體現在此時這個小根堆上，就是把堆頂元素和尾巴一交換。

那為什么每次交換完，需要我尾巴元素不能動，去構建剩余元素呢？你每構建完一次小根堆，交換元素，你此時在數組上是不是把最小的元素放在末尾了，說明已經確定了，那我們就不需要動了，我們要動的就是數組那些沒確定的元素，在這些里面去找一個最小的。那么這一步體現在堆上，是不是需要我們重新再除了尾巴元素以外剩下結點上從局部到整體去構建小根堆了。

再一次構建，是不是這里面最小的跑到堆頂了（數組里就是最小的跑到了首元素位置），再去交換首元素和沒有排好序的這一段數組的最后一個下標位置，交互完了再重構.....

舉個例子，6,2,1,4? ?這么一組數我們第一次構建小根堆之后，1就跑到了堆頂，也就是跑到了數組首元素1，數組此時為1 * * *，和最后一個元素交換，就成了* * * 1，那么這個時候1就已經確定了，我們下來要做的是把* * *這三個構建出一個小根堆，這三個里最小的放在首元素，

比方說是2 * * 1，我們交換2和這次沒確定的數組最后一個元素，成了* * 2 1，此時2 和1已經確定了，我們再去剩下兩個* *去構建，去交換，最后得到 6 4 2 1

還是這三步：

1. 把無序的這一串數，想象成一個堆，根據要求去從局部到整體構建一個大頂堆或者小頂堆，我們要的就是此時這個堆頂元素
2. 把堆頂元素和末尾元素交換，就是把堆頂元素（數組首元素）換到了數組的末端
3. 重新調整除了數組末端(已經確定順序的元素)以外的元素，去構建堆，然后交換堆頂和當前末尾，構建，交換堆頂和當前末尾..

給個小根堆的測試代碼

void FF(vector& nums, int start, int end)//構建最小堆
{
	int i = start, j = 2*i+1;
	int tmp = nums[i];
	while (j<=end)
	{
		if (j< end&& nums[j] >nums[j + 1]) j += 1;
		if (tmp<= nums[j])break;
		nums[i] = nums[j];
		i = j;
		j = i * 2 + 1;
	}
	nums[i] = tmp;
}
void SortFF(vector&nums, int n)//堆排序
{
	//if ( nums.size()==0||n< 2)return;
	int pos = (((n - 1) - 1) / 2);
	while (pos >= 0)//從下往上局部，最后整體去調整成小頂堆
	{
		FF(nums, pos,n - 1);
		pos-=1;
	}
	//調整完了此時這個二叉堆最上面就是最小的數
	//在數組里就是一頓調整之后，第一個元素是最小的

	pos = n - 1;//讓pos指向數組最后一個位置
	while (pos >0)
	{
		swap(nums[0], nums[pos]);//交換第一個元素和pos指向的位置第一次完了之后，最小元素就在數組最后
		pos-=1;    //讓pos指向數組往前一個位置，相當于最后一個元素是最小的已經確認
		FF(nums,0,pos);//那么就是開始重新調整除過已經確認元素剩下那一段數組元素
		                 //這下又把這一段數組里面最小的放在堆頂
		                 //再次進入循環，去交換位置	                
	}
}

int main()
{
	vectorvv{53,17,78,9,45,65,87,23};
	
	SortFF(vv,vv.size());
	for (auto const& x : vv) {
		cout<< x<< " ";
	}
	return 0;
}

就到這里了，我大白話把整個過程描述了一遍

你是否還在尋找穩定的海外服務器提供商？創新互聯www.cdcxhl.cn海外機房具備T級流量清洗系統配攻擊溯源，準確流量調度確保服務器高可用性，企業級服務器適合批量采購，新人活動首月15元起，快前往官網查看詳情吧

名稱欄目：堆排序詳細圖解（通俗易懂）-創新互聯
當前路徑：http://vcdvsql.cn/article14/pppge.html

成都網站建設公司_創新互聯，為您提供App設計、定制網站、動態網站、網站導航、搜索引擎優化、網站收錄

廣告

聲明：本網站發布的內容（圖片、視頻和文字）以用戶投稿、用戶轉載內容為主，如果涉及侵權請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網站立場，如需處理請聯系客服。電話：028-86922220；郵箱：631063699@qq.com。內容未經允許不得轉載，或轉載時需注明來源： 創新互聯