本篇文章為大家展示了如何在Python怎么中使用heapq模塊，內(nèi)容簡明扼要并且容易理解，絕對能使你眼前一亮，通過這篇文章的詳細(xì)介紹希望你能有所收獲。

成都創(chuàng)新互聯(lián)公司長期為上1000+客戶提供的網(wǎng)站建設(shè)服務(wù)，團(tuán)隊(duì)從業(yè)經(jīng)驗(yàn)10年，關(guān)注不同地域、不同群體，并針對不同對象提供差異化的產(chǎn)品和服務(wù)；打造開放共贏平臺(tái)，與合作伙伴共同營造健康的互聯(lián)網(wǎng)生態(tài)環(huán)境。為灤州企業(yè)提供專業(yè)的做網(wǎng)站、成都網(wǎng)站制作，灤州網(wǎng)站改版等技術(shù)服務(wù)。擁有十多年豐富建站經(jīng)驗(yàn)和眾多成功案例,為您定制開發(fā)。

heapq 模塊實(shí)現(xiàn)了適用于Python列表的最小堆排序算法。

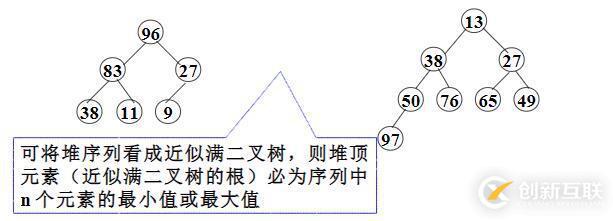
堆是一個(gè)樹狀的數(shù)據(jù)結(jié)構(gòu)，其中的子節(jié)點(diǎn)都與父母排序順序關(guān)系。因?yàn)槎雅判蛑械臉涫菨M二叉樹，因此可以用列表來表示樹的結(jié)構(gòu)，使得元素 N 的子元素位于 2N + 1 和 2N + 2 的位置（對于從零開始的索引）。

本文內(nèi)容將分為三個(gè)部分，第一個(gè)部分簡單介紹 heapq 模塊的使用；第二部分回顧堆排序算法；第三部分分析heapq中的實(shí)現(xiàn)。

heapq 的使用

創(chuàng)建堆有兩個(gè)基本的方法：heappush() 和 heapify()，取出堆頂元素用 heappop()。

heappush() 是用來向已有的堆中添加元素，一般從空列表開始構(gòu)建：

import heapq

data = [97, 38, 27, 50, 76, 65, 49, 13]
heap = []

for n in data:
 heapq.heappush(heap, n)

print('pop:', heapq.heappop(heap)) # pop: 13
print(heap) # [27, 50, 38, 97, 76, 65, 49]

如果數(shù)據(jù)已經(jīng)在列表中，則使用 heapify() 進(jìn)行重排：

import heapq

data = [97, 38, 27, 50, 76, 65, 49, 13]

heapq.heapify(data)

print('pop:', heapq.heappop(data)) # pop: 13
print(data) # [27, 38, 49, 50, 76, 65, 97]

回顧堆排序算法

堆排序算法基本思想是：將無序序列建成一個(gè)堆，得到關(guān)鍵字最小（或大的記錄；輸出堆頂?shù)淖钚?（大）值后，使剩余的 n-1 個(gè)元素 重又建成一個(gè)堆，則可得到n個(gè)元素的次小值 ；重復(fù)執(zhí)行，得到一個(gè)有序序列，這個(gè)就是堆排序的過程。

堆排序需要解決兩個(gè)問題：

• 如何由一個(gè)無序序列建立成一個(gè)堆？

• 如何在輸出堆頂元素之后，調(diào)整剩余元素，使之成為一個(gè)新的堆？

• 新添加元素和，如何調(diào)整堆？

先來看看第二個(gè)問題的解決方法。采用的方法叫“篩選”，當(dāng)輸出堆頂元素之后，就將堆中最后一個(gè)元素代替之；然后將根結(jié)點(diǎn)值與左、右子樹的根結(jié)點(diǎn)值進(jìn)行比較 ，并與其中小者進(jìn)行交換；重復(fù)上述操作，直至葉子結(jié)點(diǎn)，將得到新的堆，稱這個(gè)從堆頂至葉子的調(diào)整過程為“篩選”。

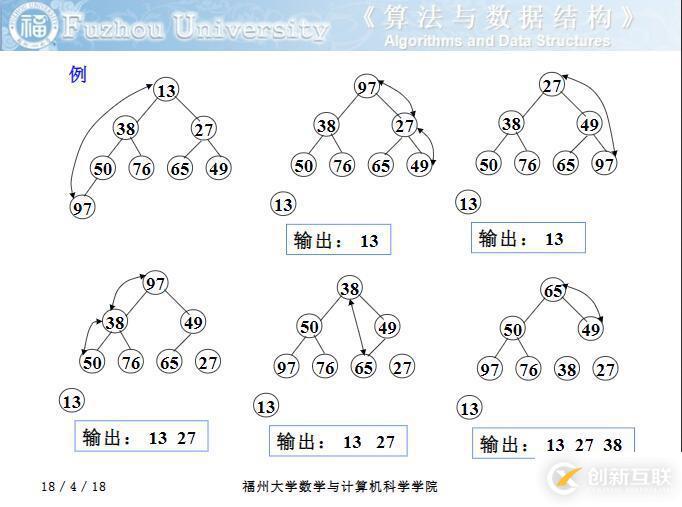
如上圖所示，當(dāng)堆頂 13 輸出后，將堆中末尾的 97 替代為堆頂，然后堆頂與它的子節(jié)點(diǎn) 38 和 27 中的小者交換；元素 97 在新的位置上在和它的子節(jié)點(diǎn) 65 和 49 中的小者交換；直到元素97成為葉節(jié)點(diǎn)，就得到了新的堆。這個(gè)過程也叫 下沉 。

讓堆中位置為 pos 元素進(jìn)行下沉的如下：

def heapdown(heap, pos):
 endpos = len(heap)
 while pos < endpos:
 lchild = 2 * pos + 1
 rchild = 2 * pos + 2
 if lchild >= endpos: # 如果pos已經(jīng)是葉節(jié)點(diǎn)，退出循環(huán)
  break
 childpos = lchild # 假設(shè)要交換的節(jié)點(diǎn)是左節(jié)點(diǎn)
 if rchild < endpos and heap[childpos] > heap[rchild]:
  childpos = rchild

 if heap[pos] < heap[childpos]: # 如果節(jié)點(diǎn)比子節(jié)點(diǎn)都小，退出循環(huán)
  break
 heap[pos], heap[childpos] = heap[childpos], heap[pos] # 交換
 pos = childpos

再來看看如何解決第三個(gè)問題：新添加元素和，如何調(diào)整堆？這個(gè)的方法正好與 下沉 相反，首先將新元素放置列表的最后，然后新元素與其父節(jié)點(diǎn)比較，若比父節(jié)點(diǎn)小，與父節(jié)點(diǎn)交換；重復(fù)過程直到比父節(jié)點(diǎn)大或到根節(jié)點(diǎn)。這個(gè)過程使得元素從底部不斷上升，從下至上恢復(fù)堆的順序，稱為 上浮 。

將位置為 pos 進(jìn)行上浮的代碼為：

def heapup(heap, startpos, pos): # 如果是新增元素，startpos 傳入 0
 while pos > startpos:
 parentpos = (pos - 1) // 2
 if heap[pos] < heap[parentpos]:
  heap[pos], heap[parentpos] = heap[parentpos], heap[pos]
  pos = parentpos
 else:
  break

第一個(gè)問題：如何由一個(gè)無序序列建立成一個(gè)堆？從無序序列的第 n/2 個(gè)元素 （即此無序序列對應(yīng)的完全二叉樹的最后一個(gè)非終端結(jié)點(diǎn) ）起 ，至第一個(gè)元素止，依次進(jìn)行下沉：

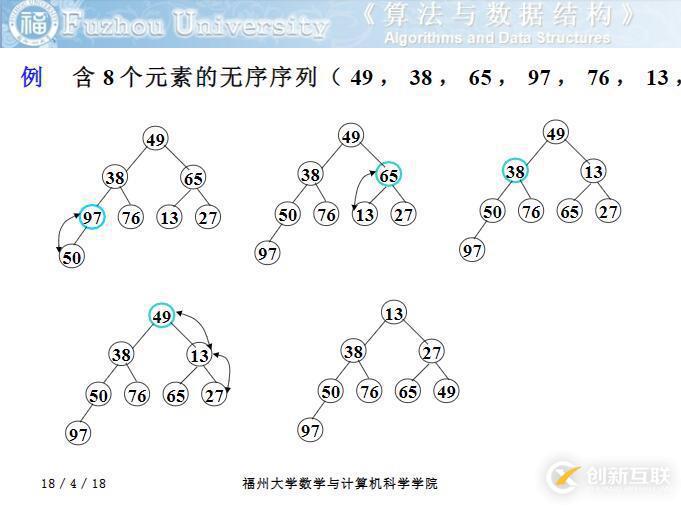
for i in reversed(range(len(data) // 2)):
 heapdown(data, i)

heapq 源碼分析

添加新元素到堆中的 heappush() 函數(shù)：

def heappush(heap, item):
 """Push item onto heap, maintaining the heap invariant."""
 heap.append(item)
 _siftdown(heap, 0, len(heap)-1)

把目標(biāo)元素放置列表最后，然后進(jìn)行上浮。盡管它命名叫 down ,但這個(gè)過程是上浮的過程，這個(gè)命名也讓我困惑，后來我才知道它是因?yàn)樵氐乃饕粩鄿p小，所以命名 down 。下沉的過程它也就命名為 up 了。

def _siftdown(heap, startpos, pos):
 newitem = heap[pos]
 # Follow the path to the root, moving parents down until finding a place
 # newitem fits.
 while pos > startpos:
  parentpos = (pos - 1) >> 1
  parent = heap[parentpos]
  if newitem < parent:
   heap[pos] = parent
   pos = parentpos
   continue
  break
 heap[pos] = newitem

一樣是通過 newitem 不斷與父節(jié)點(diǎn)比較。不一樣的是這里缺少了元素交換的過程，而是計(jì)算出新元素最后所在的位置 pos 并進(jìn)行的賦值。顯然這是優(yōu)化后的代碼，減少了不斷交換元素的冗余過程。

再來看看輸出堆頂元素的函數(shù) heappop():

def heappop(heap):
 """Pop the smallest item off the heap, maintaining the heap invariant."""
 lastelt = heap.pop() # raises appropriate IndexError if heap is empty
 if heap:
  returnitem = heap[0]
  heap[0] = lastelt
  _siftup(heap, 0)
  return returnitem
 return lastelt

通過 heap.pop() 獲得列表中的最后一個(gè)元素，然后替換為堆頂 heap[0] = lastelt ，再進(jìn)行下沉：

def _siftup(heap, pos):
 endpos = len(heap)
 startpos = pos
 newitem = heap[pos]
 # Bubble up the smaller child until hitting a leaf.
 childpos = 2*pos + 1 # 左節(jié)點(diǎn)，默認(rèn)替換左節(jié)點(diǎn)
 while childpos < endpos:
  # Set childpos to index of smaller child.
  rightpos = childpos + 1 # 右節(jié)點(diǎn)
  if rightpos < endpos and not heap[childpos] < heap[rightpos]:
   childpos = rightpos # 當(dāng)右節(jié)點(diǎn)比較小時(shí)，應(yīng)交換的是右節(jié)點(diǎn)
  # Move the smaller child up.
  heap[pos] = heap[childpos]
  pos = childpos
  childpos = 2*pos + 1
 # The leaf at pos is empty now. Put newitem there, and bubble it up
 # to its final resting place (by sifting its parents down).
 heap[pos] = newitem
 _siftdown(heap, startpos, pos)

這邊的代碼將準(zhǔn)備要下沉的元素視為新元素 newitem ，將其當(dāng)前的位置 pos 視為空位置，由其子節(jié)點(diǎn)中的小者進(jìn)行取代，反復(fù)如此，最后會(huì)在葉節(jié)點(diǎn)留出一個(gè)位置，這個(gè)位置放入 newitem ，再讓新元素進(jìn)行上浮。

再來看看讓無序數(shù)列重排成堆的 heapify() 函數(shù)：

def heapify(x):
 """Transform list into a heap, in-place, in O(len(x)) time."""
 n = len(x)
 for i in reversed(range(n//2)):
  _siftup(x, i)

上述內(nèi)容就是如何在Python怎么中使用heapq模塊，你們學(xué)到知識(shí)或技能了嗎？如果還想學(xué)到更多技能或者豐富自己的知識(shí)儲(chǔ)備，歡迎關(guān)注創(chuàng)新互聯(lián)行業(yè)資訊頻道。

文章標(biāo)題：如何在Python怎么中使用heapq模塊-創(chuàng)新互聯(lián)
瀏覽地址：http://vcdvsql.cn/article20/cecico.html

成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián)，為您提供營銷型網(wǎng)站建設(shè)、移動(dòng)網(wǎng)站建設(shè)、企業(yè)網(wǎng)站制作、動(dòng)態(tài)網(wǎng)站、關(guān)鍵詞優(yōu)化、ChatGPT

廣告

聲明：本網(wǎng)站發(fā)布的內(nèi)容（圖片、視頻和文字）以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主，如果涉及侵權(quán)請盡快告知，我們將會(huì)在第一時(shí)間刪除。文章觀點(diǎn)不代表本網(wǎng)站立場，如需處理請聯(lián)系客服。電話：028-86922220；郵箱：631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載，或轉(zhuǎn)載時(shí)需注明來源： 創(chuàng)新互聯(lián)