C++中如何實現搜索二叉樹-創新互聯
本篇內容介紹了“C++中如何實現搜索二叉樹”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!

二叉查找樹(英語:Binary Search Tree),也稱二叉搜索樹、有序二叉樹(英語:ordered binary tree),排序二叉樹(英語:sorted binary tree),是指一棵空樹或者具有下列性質的二叉樹:
任意節點的左子樹不空,則左子樹上所有結點的值均小于它的根結點的值;
任意節點的右子樹不空,則右子樹上所有結點的值均大于它的根結點的值;
任意節點的左、右子樹也分別為二叉查找樹;
沒有鍵值相等的節點。
#pragma once
template<class K, class V>
struct BSTreeNode
{
K _key;
V _value;
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
BSTreeNode(const K& key, const V& value)
:_key(key)
,_value(value)
,_left(NULL)
,_right(NULL)
{}
};
template<class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
BSTree()
:_root(NULL)
{}
bool Insert(const K& key, const V& value)
{
if (NULL == _root)//若為空樹
{
_root = new Node(key, value);
return true;
}
Node* parent = NULL;
Node* cur = _root;
//確定插入節點的位置
while (cur)
{
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else//已經存在key
{
return false;
}
}
//插入節點
if (key > parent->_key)
parent->_right = new Node(key, value);
else
parent->_left = new Node(key, value);
}
//Insert遞歸寫法
bool InsertR(const K& key, const V& value)
{
return _InsertR(_root, key, value);
}
bool _InsertR(Node*& root, const K& key, const V& value)
{
if (NULL == root)
{
root = new Node(key, value);
return true;
}
if (key > root->_key)
return _InsertR(root->_right, key, value);
else if (key < root->_key)
return _InsertR(root->_left, key, value);
else
return false;
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (key > cur->_key)
cur = cur->_right;
else if (key < cur->_key)
cur = cur->_left;
else
return cur;
}
return NULL;
}
//Find遞歸寫法
Node* FindR(const K& key)
{
return _FindR(_root, key);
}
Node* _FindR(Node* root, const K& key)
{
if (NULL == root)
return NULL;
if (key > root->_key)
return _FindR(root->_right, key);
else if (key < root->_key)
return _FindR(root->_left, key);
else
return root;
}
bool Remove(const K& key)
{
Node* parent = NULL;
Node* cur = _root;
//確定刪除節點的位置
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
break;
}
}
if (NULL == cur)//沒有該節點
{
return false;
}
Node* del;
if (NULL == cur->_left)//刪除節點的左孩子為空
{
del = cur;
//刪除的節點為根節點
if (NULL == parent)
{
_root = _root->_right;
}
else
{
if (cur == parent->_left)
parent->_left = cur->_right;
else
parent->_right = cur->_right;
}
}
else if (NULL == cur->_right)//刪除節點的右孩子為空
{
del = cur;
if (NULL == parent)
{
_root = _root->_left;
}
else
{
if (cur == parent->_left)
parent->_left = cur->_right;
else
parent->_right = cur->_left;
}
}
else//刪除節點的左右孩子都不為空,找右子樹最左節點代替該節點刪除
{
parent = cur;
Node* leftmost = cur->_right;
while (leftmost->_left)
{
parent = leftmost;
leftmost = leftmost->_left;
}
del = leftmost;
cur->_key = leftmost->_key;
cur->_value = leftmost->_value;
if (leftmost == parent->_left)
parent->_left = leftmost->_right;
else
parent->_right = leftmost->_right;
}
return true;
}
//Remove遞歸寫法
bool RemoveR(const K& key)
{
return _RemoveR(_root, key);
}
bool _RemoveR(Node*& root, const K& key)
{
if (NULL == root)
return false;
if (key > root->_key)
{
return _RemoveR(root->_right, key);
}
else if (key < root->_key)
{
return _RemoveR(root->_left, key);
}
else
{
Node* del = root;
if (NULL == root->_left)
{
root = root->_right;
}
else if (NULL == root->_right)
{
root = root->_left;
}
else
{
Node* leftmost = root->_right;
while (leftmost->_left)
{
leftmost = leftmost->_left;
}
swap(root->_key, leftmost->_key);
swap(root->_value, leftmost->_value);
return _RemoveR(root->_right, key);
}
delete del;
}
return true;
}
//中序遍歷遞歸寫法
void InOrder()
{
_InOrder(_root);
}
void _InOrder(Node* root)
{
if (NULL == root)
return;
_InOrder(root->_left);
cout<<root->_key<<" ";
_InOrder(root->_right);
}
protected:
Node* _root;
};
void Test()
{
BSTree<int, int> t;
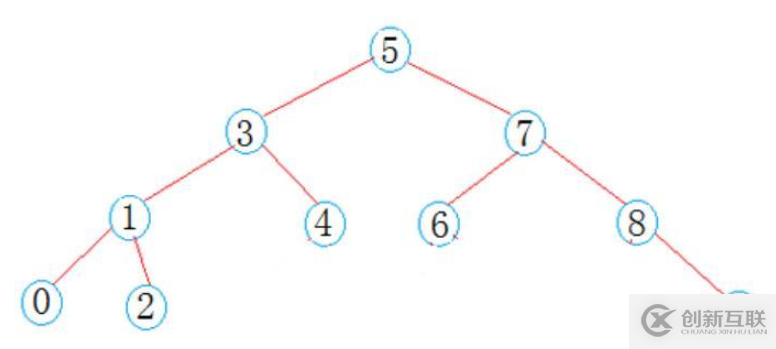
int a[] = {5, 3, 4, 1, 7, 8, 2, 6, 0, 9};
for (size_t i = 0; i < sizeof(a)/sizeof(a[0]);++i)
{
t.InsertR(a[i], i);
}
cout<<t.FindR(8)->_key<<endl;
cout<<t.FindR(5)->_key<<endl;
cout<<t.FindR(9)->_key<<endl;
t.RemoveR(8);
t.RemoveR(7);
t.RemoveR(9);
t.RemoveR(6);
t.RemoveR(5);
t.RemoveR(3);
t.RemoveR(1);
t.RemoveR(4);
t.RemoveR(0);
t.RemoveR(2);
t.InOrder();
}
“C++中如何實現搜索二叉樹”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注創新互聯網站,小編將為大家輸出更多高質量的實用文章!
分享標題:C++中如何實現搜索二叉樹-創新互聯
標題來源:http://vcdvsql.cn/article20/dsdjco.html
成都網站建設公司_創新互聯,為您提供移動網站建設、標簽優化、App開發、做網站、搜索引擎優化、虛擬主機
聲明:本網站發布的內容(圖片、視頻和文字)以用戶投稿、用戶轉載內容為主,如果涉及侵權請盡快告知,我們將會在第一時間刪除。文章觀點不代表本網站立場,如需處理請聯系客服。電話:028-86922220;郵箱:631063699@qq.com。內容未經允許不得轉載,或轉載時需注明來源: 創新互聯

- 品牌網站建設從內容的角度開始嗎? 2020-12-16
- 企業該如何選擇品牌網站建設供應商? 2016-02-04
- 品牌網站建設抓住幾點 2022-12-04
- 創新互聯私人訂制品牌網站建設 2015-06-04
- 所謂品牌網站建設沒有我們想的簡單與復雜! 2022-08-22
- 高端品牌網站建設需要注意哪些問題 2018-05-01
- 品牌網站建設公司哪家好? 2016-09-19
- 高端品牌網站建設定制網站優化上上策 2022-08-08
- 中小企業品牌網站建設與塑造 2022-01-25
- 品牌網站建設什么內容重要? 2022-03-22
- 品牌網站建設與普通的網站制作有何區別呢? 2016-11-12
- 品牌網站建設中小企業要如何才能實現品牌網站的建設 2023-03-20