[數(shù)據(jù)結(jié)構(gòu)]二叉樹--堆-創(chuàng)新互聯(lián)

- 什么是堆
- 堆的實現(xiàn)
- 類的定義
- 構(gòu)造函數(shù)
- 析構(gòu)函數(shù)
- push
- 向上調(diào)整
- 判斷堆是否為空
- 返回堆中有效數(shù)據(jù)個數(shù)
- 返回堆頂?shù)臄?shù)據(jù)
- pop數(shù)據(jù),刪除堆頂?shù)臄?shù)據(jù)
- 向下調(diào)整
- 堆的應(yīng)用
- TopK問題
- 堆排序
- 1.第一種建堆方式-->向上調(diào)整
- 2.第二種建堆方式--->向下調(diào)整
- 排序
- 總結(jié)
注意大家在學(xué)習(xí)編程的過程中, 肯定聽說過內(nèi)存中的堆和棧以及靜態(tài)區(qū)這種的, 這些是屬于操作系統(tǒng)虛擬進程地址空間中的,
我們要說的堆和這個并不是一回事,堆是二叉樹的一種, 是數(shù)據(jù)結(jié)構(gòu)的一種,我們來看看吧
普通的二叉樹不使用數(shù)組來存儲,只有堆用數(shù)組來存儲,
所以說堆的邏輯結(jié)構(gòu)是二叉樹, 物理結(jié)構(gòu)是數(shù)組
如果有一個關(guān)鍵碼的集合K = { , , ,…, },把它的所有元素按完全二叉樹的順序存儲方式存儲,在一個一維數(shù)組中,并滿足:<= 且<= ( >= 且 >= ) i = 0,1,2…,則稱為小堆(或大堆)。將根節(jié)點大的堆叫做大堆或大根堆,根節(jié)點最小的堆叫做最小堆或小根堆
堆的性質(zhì):
- 堆中某個節(jié)點的值總是不大于或不小于其父節(jié)點的值;
- 堆總是一棵完全二叉樹。
小堆: 子節(jié)點都比不小于父節(jié)點

大堆
堆的實現(xiàn)那我們嘗試用數(shù)組來實現(xiàn)這種數(shù)據(jù)結(jié)構(gòu)
類的定義那我們來分析一下堆這個類中需要哪些成員,
templateclass Heap
{public:
Heap();
void push(T val);
void pop();
T Top();
bool empty();
size_t size();
~Heap();
private:
T* _data;
int _top;//指向最后一個數(shù)據(jù)的下一個位置
int _capacity;
}; 默認構(gòu)造就是把成員都初始化一下,我這里沒有開默認空間, 大家可以選擇開
Heap()
:_data(nullptr)
, _top(0)
, _capacity(0)
{}
析構(gòu)函數(shù)進行資源清理,所以要把申請的空間都釋放掉
~Heap()
{free(_data);
_top = _capactiy = 0;
}push就是插入一個數(shù)據(jù),堆這里的插入和其他數(shù)據(jù)結(jié)構(gòu)不同, 堆插入任何一個數(shù)據(jù)都要保證堆的特性, 不可以本來是堆,最后不是堆, 我們來分析一下,我們這里都以建大堆為例子
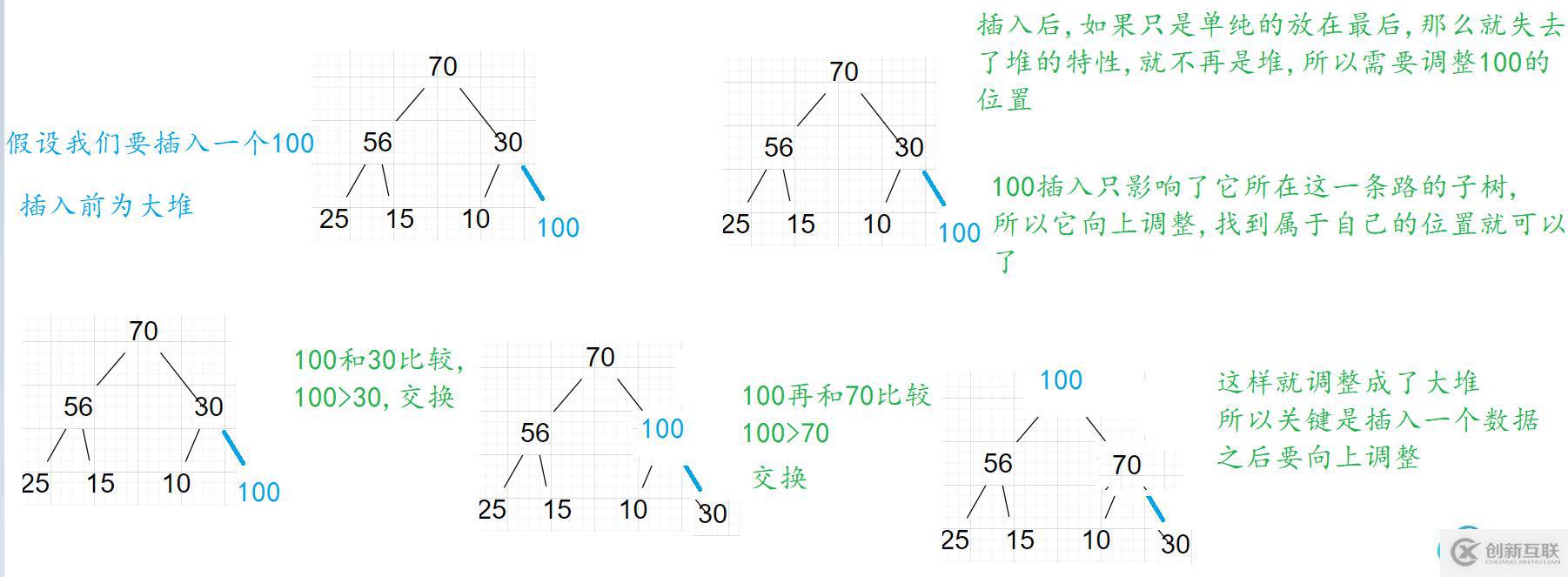
插入的代碼比較簡單,關(guān)鍵是向上調(diào)整,插入唯一需要注意的就是擴容的問題
void push(T val)
{//如果容量 == 個數(shù)
if (_capacity == _top)
{//擴容 -- >2倍擴容
int newCapacity = _capacity == 0 ? 4 : _capacity * 2;
T* ptr = (T*)realloc(_data, sizeof(T) * newCapacity);
if (nullptr == ptr)
{ perror("realloc fail");
exit(-1);
}
_capacity = newCapacity;
_data = ptr;
}
//擴容完畢
_data[_top] = val;
//++ 長度
++_top;
//向上調(diào)整
AdjustUp(_data, _top - 1);
}
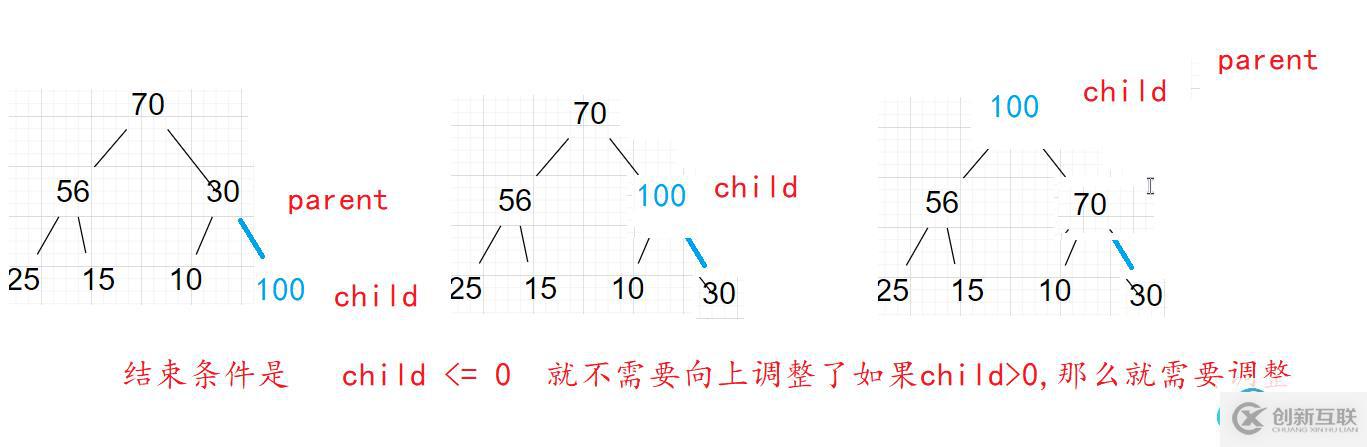
為了保證堆的特性而向上調(diào)整,

那我們來分析一下這個向上調(diào)整該如何實現(xiàn)
void AdjustUp(T* data, int child)
{int parent = (child - 1) / 2;
while (child >0)
{ //這里是以大堆為例,如果孩子大于父親, 那么就調(diào)整
if (data[child] >data[parent])
{ swap(data[child], data[parent]);
//迭代
child = parent;
parent = (child - 1) / 2;
}
else
{ break;
}
}這個相對比較簡單
bool empty()
{//如果top等于0為空
return _top == 0;
}size_t size()
{return _top;
}首先要判斷堆是否為空, 如果堆不為空, 還取個啥啊
T Top()
{assert(!empty());
return _data[_top - 1];
}我們來分析一下

void pop()
{assert(!empty());
//交換堆頂?shù)臄?shù)據(jù)和最后一個數(shù)據(jù)
swap(_data[0], _data[_top - 1]);
--_top;
//向下調(diào)整
AdjustDown(_data, n, 0);
}
核心思想就是如果大孩子大于根節(jié)點, 就交換,直到最后歐一層
void AdjustDown(T* data, int n, int parent)
{//先給出左孩子
int child = parent * 2 + 1;
while (child< n)
{ //如果右孩子存在,并且比左孩子大
if (child + 1< n && data[child + 1] >data[child])
child++;
if (data[child] >data[parent])
{ swap(data[child], data[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{ break;
}
}
}堆排序關(guān)于TopK問題,用堆解決是非常合適的問題,我之前寫過一篇 TopK問題詳解
堆排序是一種非常厲害的排序, 核心思想就利用了堆這種數(shù)據(jù)結(jié)構(gòu),我們來看看吧,我們距離
如果排升序的話,我們建小堆還是大堆呢??我們來分析一下
那我們該如何建堆呢?
插入建堆
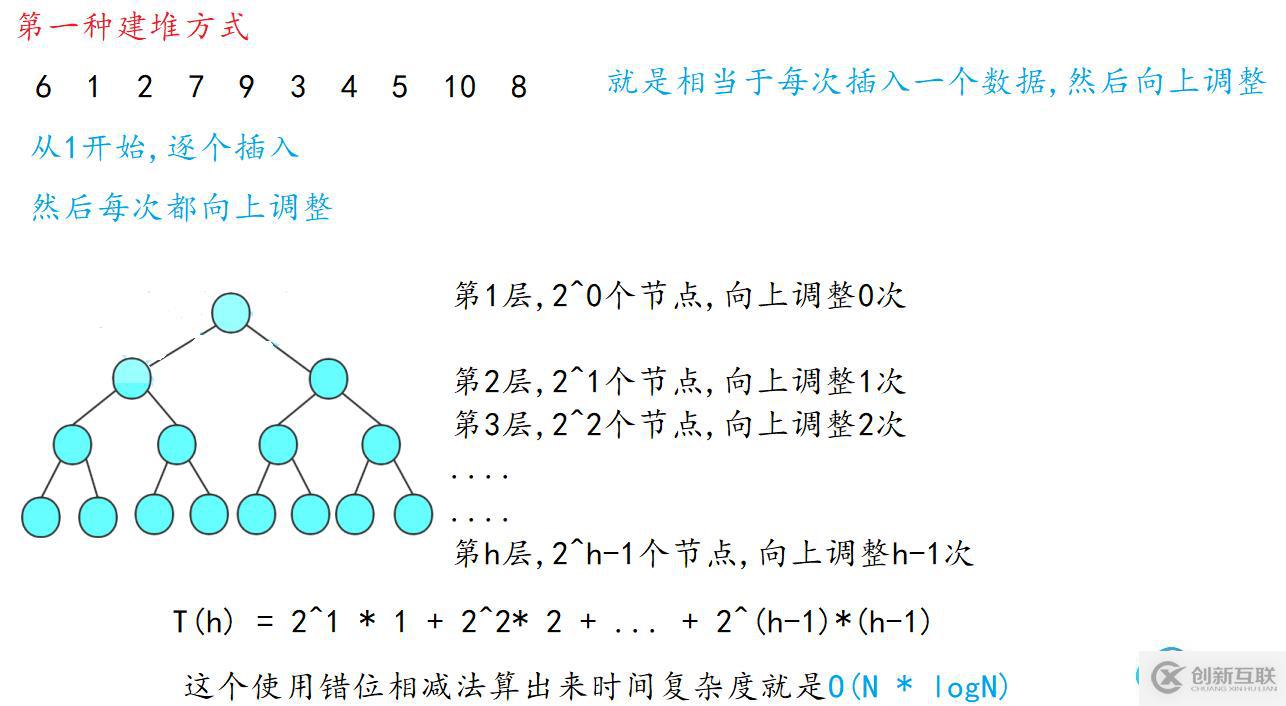
int arr[] = {6,1,2,7,9,3,4,5,10,8 };
int len = sizeof(arr) / sizeof(int);
for (int i = 1; i< len; ++i)
{AdjustUp(arr, i);
}向下調(diào)整建堆就是二叉樹的典型分治思想,我們來分析一下
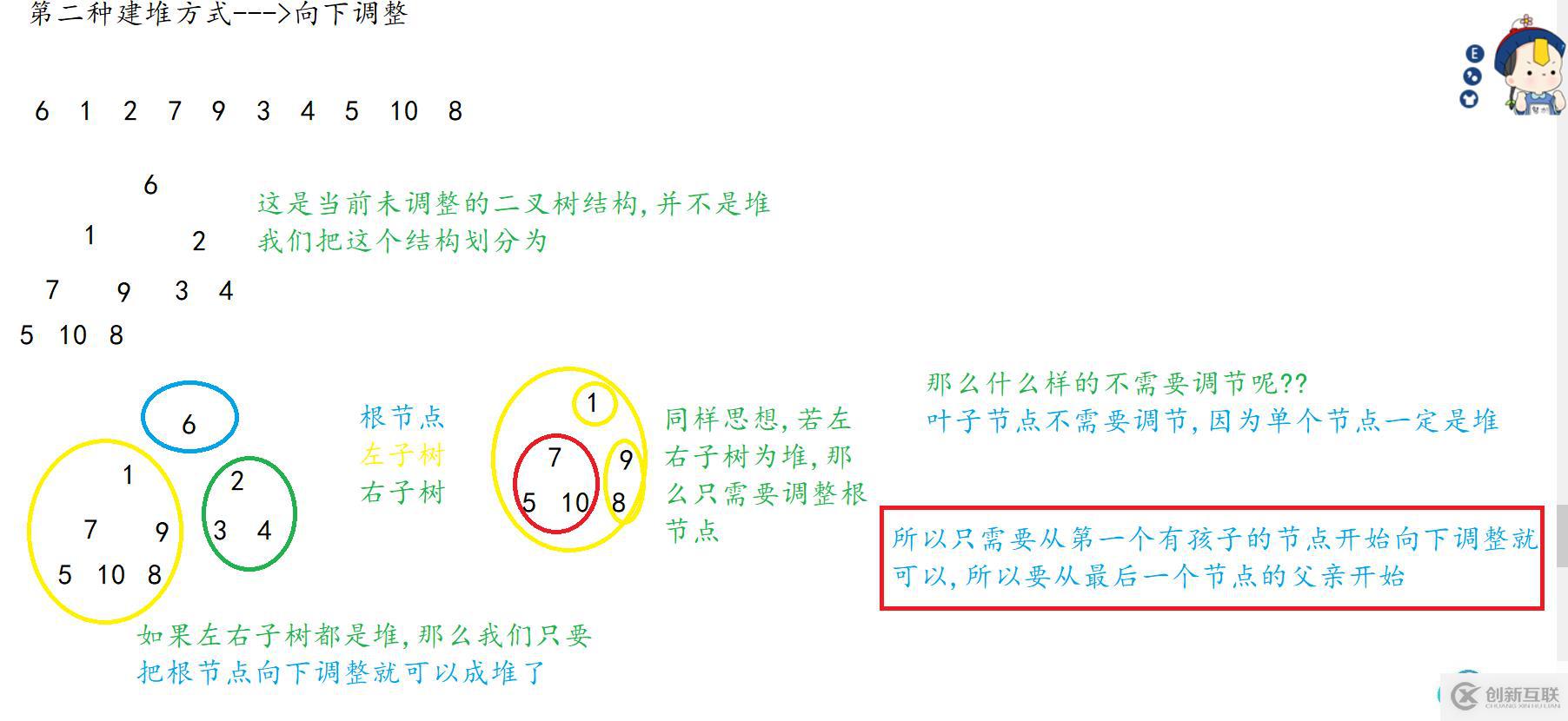
int arr[] = {6,1,2,7,9,3,4,5,10,8 };
int len = sizeof(arr) / sizeof(int);
//建堆 最后一個節(jié)點的下標(biāo)是len-1 ,所以它的父親下標(biāo)是(len-2)/2
for (int i = (len - 1 - 1) / 2; i >= 0; --i)
{AdjustDown(arr, len, i);
}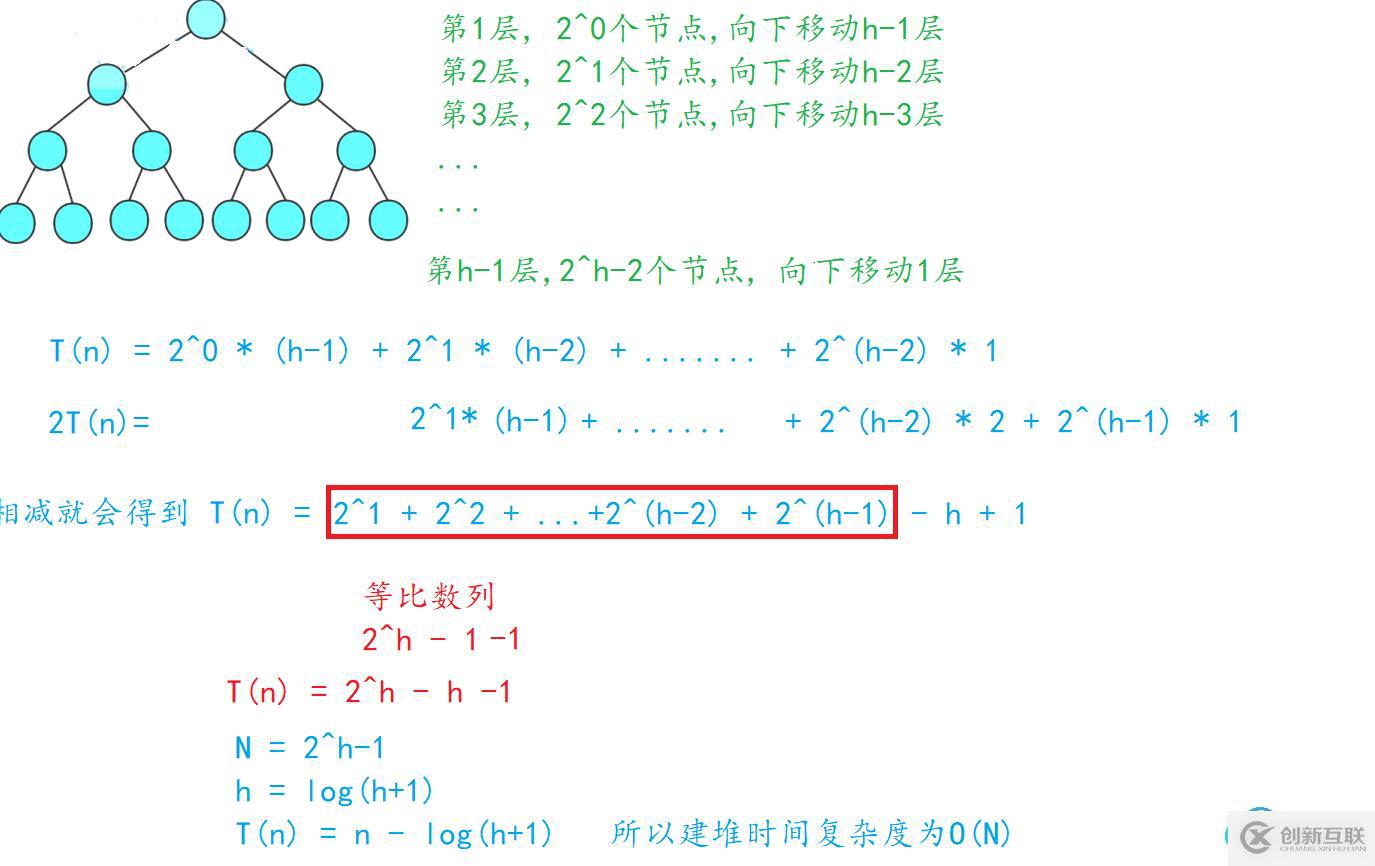
排序所以更推薦使用向下調(diào)整的方式來建堆,因為復(fù)雜度比較低
建好堆了以后就相對比較簡單了,
利用堆的特性, pop的思想,把大的放到最后面, 然后調(diào)整前面的
void HeapSort(int* arr, int len)
{//建堆
for (int i = (len - 1 - 1) / 2; i >= 0; --i)
{AdjustDown(arr, len, i);
}
int end = len - 1;
while (end >0)
{swap(arr[0], arr[end]);
AdjustDown(arr, end, 0);
--end;
}
}建堆的復(fù)雜度O(N) , 調(diào)整的復(fù)雜度O(N* logN)
所以堆排序的復(fù)雜度就是O(N*logN)
總結(jié)堆還是非常常用的,一定要利用堆的特性, 后面的優(yōu)先級隊列還會涉及到,
感謝收看
你是否還在尋找穩(wěn)定的海外服務(wù)器提供商?創(chuàng)新互聯(lián)www.cdcxhl.cn海外機房具備T級流量清洗系統(tǒng)配攻擊溯源,準(zhǔn)確流量調(diào)度確保服務(wù)器高可用性,企業(yè)級服務(wù)器適合批量采購,新人活動首月15元起,快前往官網(wǎng)查看詳情吧
當(dāng)前題目:[數(shù)據(jù)結(jié)構(gòu)]二叉樹--堆-創(chuàng)新互聯(lián)
轉(zhuǎn)載來源:http://vcdvsql.cn/article24/ceedce.html
成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián),為您提供用戶體驗、動態(tài)網(wǎng)站、網(wǎng)站內(nèi)鏈、云服務(wù)器、電子商務(wù)、服務(wù)器托管
聲明:本網(wǎng)站發(fā)布的內(nèi)容(圖片、視頻和文字)以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主,如果涉及侵權(quán)請盡快告知,我們將會在第一時間刪除。文章觀點不代表本網(wǎng)站立場,如需處理請聯(lián)系客服。電話:028-86922220;郵箱:631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載,或轉(zhuǎn)載時需注明來源: 創(chuàng)新互聯(lián)
猜你還喜歡下面的內(nèi)容
- php中處理websocket的流程和方法-創(chuàng)新互聯(lián)
- 利用HTML5+CSS3打造支持語音輸入的搜索框-創(chuàng)新互聯(lián)
- 用代碼實例分析Python如何基于pandas繪制散點圖矩陣-創(chuàng)新互聯(lián)
- 微信開發(fā)—帶參數(shù)二維碼的使用方法-創(chuàng)新互聯(lián)
- golang代碼生成Go語言現(xiàn)在的前景怎么樣?-創(chuàng)新互聯(lián)
- php設(shè)計模式總結(jié)上-創(chuàng)新互聯(lián)
- python中的map如何使用-創(chuàng)新互聯(lián)

- 開展全網(wǎng)營銷推廣的5個步驟 2016-11-11
- 全網(wǎng)營銷怎么做才有效果呢? 2014-07-08
- 全網(wǎng)營銷可以從哪些地方著手呢? 2014-07-07
- 如何實現(xiàn)全網(wǎng)營銷? 2015-08-08
- 成都全網(wǎng)營銷推廣方式有哪些? 2016-11-11
- 全網(wǎng)營銷是什么?中小企業(yè)應(yīng)如何做好全網(wǎng)營銷? 2016-11-09
- 機械設(shè)備行業(yè)如何做好全網(wǎng)營銷好 2014-04-20
- 新聞營銷對于全網(wǎng)營銷推廣重要嗎? 2015-10-20
- 企業(yè)全網(wǎng)營銷型網(wǎng)站建設(shè)的重點有哪一些? 2016-11-07
- 全網(wǎng)營銷推廣,讓成交變得簡單 2016-11-08
- 全網(wǎng)營銷型網(wǎng)站助企業(yè)決勝未來 2014-04-05
- 全網(wǎng)營銷時代網(wǎng)絡(luò)營銷基本要素環(huán)節(jié)有哪些需要特別注意 2016-08-17