數據結構--‘搜索二叉樹’-創新互聯
‘二叉樹’是數據結構中比較重要的一部分,這里主要討論一下‘搜索二叉樹’,針對‘搜索二叉樹的插入、刪除和查找節點進行分情況討論,希望能夠幫助讀者更加的理解搜索二叉樹的原理。
目前創新互聯公司已為上1000+的企業提供了網站建設、域名、虛擬主機、網站托管維護、企業網站設計、科爾沁右翼中網站維護等服務,公司將堅持客戶導向、應用為本的策略,正道將秉承"和諧、參與、激情"的文化,與客戶和合作伙伴齊心協力一起成長,共同發展。◆搜索二叉樹的性質:
1.每個節點都有一個一個作為搜索依據的關鍵碼,所有節點的關鍵碼都不相同。
2.左子樹所有的關鍵碼(key)都小于根節點的關鍵碼(key)。
3.右子樹所有的關鍵碼(key)都大于根節點的關鍵碼(key)。
4.左、右子樹都是二叉搜索樹。
實現‘搜索二叉樹’的節點結構可以實現為K形式,和K、V形式,若實現K形式,則K表示節點的值,同時可以使用K來確定節點的位置,若實現K、V形式,則K表示節點的一個標記,用來判斷節點在二叉樹中具體的存儲位置,V表示節點的具體存儲的值。這里實現的是K、V形式,K形式讀者可以下去自己進行嘗試。
◆下面為實現‘搜索二叉樹’的具體節點結構:
template <class K, class V>
struct BSTNode
{
BSTNode<K, V>* _left; //指向左節點的指針
BSTNode<K, V>* _right; //指向右節點的指針
K _key; //節點標記,確定節點位置
V _value; //節點的值
BSTNode(const K& key, const V& value) //構造節點
:_key(key)
, _value(value)
, _left(NULL)
, _right(NULL)
{ }
};◆討論相關操作情況
(1)節點插入
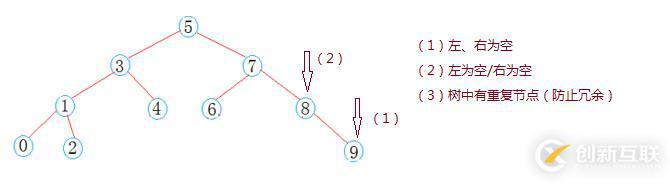
(2)節點刪除
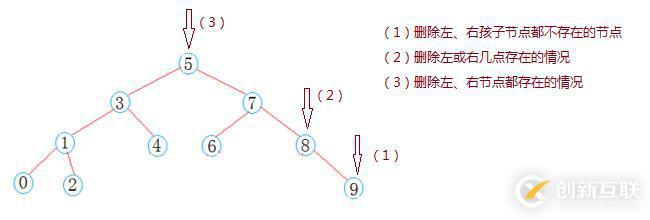
(3)節點查找
根據搜索二叉樹的性質來進行查找,當key>root->key;向右孩子節點再次進行查找,當key<root->key,從左邊的孩子節點進行查找,否則,就證明查找到了。
◆下面是詳細的代碼(實現的遞歸和非遞歸兩種方式)
template <class K, class V>
class BSTree
{
typedef BSTNode<K, V> Node;
public:
BSTree() //構造
:_root(NULL)
{}
bool Insert(const K& key, const V& value) //非遞歸插入
{
if (_root == NULL) //根節點為空
{
_root = new Node(key, value);
return true;
}
Node* cur = _root;
if (cur->_left == NULL && cur->_right == NULL) //父節點的左右節點為空
{
if (cur->_key < key)
{
cur->_right = new Node(key, value);
}
else if (cur->_key > key)
{
cur->_left = new Node(key, value);
}
else
{
return false;
}
}
else
{
Node* parent = cur;
while (cur)
{
parent = cur;
if (cur->_key < key)
{
if (parent->_right == NULL) //右節點為空
{
parent->_right = new Node(key, value);
}
cur = cur->_right;
}
else if (cur->_key > key)
{
if (parent->_left == NULL) //左節點為空
{
parent->_left = new Node(key, value);
}
cur = cur->_left;
}
else //數據在樹中已經存在,防止數據冗余
{
return false;
}
}
}
return true;
}
bool Remove(const K& key) //非遞歸刪除
{
if (_root == NULL) //根節點為空
{
return false;
}
if (_root->_left == NULL && _root->_right == NULL) //根節點的左右節點為空
{
if (_root->_key == key)
{
delete _root;
_root = NULL;
return true;
}
else
{
return false;
}
}
Node* parent = NULL;
Node* cur = _root;
while (cur)
{
if (cur->_key > key) //尋找要刪除的節點
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else //找到要刪除的節點
{
Node* del = cur;
if (cur->_left == NULL) //左為空
{
if (parent == NULL) //cur節點沒有父節點
{
_root = cur->_right;
}
else //cur有父節點
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
}
else if (cur->_right == NULL) //右為空
{
if (parent == NULL)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
}
else //左、右為空
{
//找右樹的最左節點
//找到的節點與cur交換再刪除
parent = cur;
Node* firstLeft = cur->_right;
while (firstLeft->_left)
{
parent = firstLeft;
parent = firstLeft->_left;
}
swap(cur->_key, firstLeft->_key);
swap(cur->_value, firstLeft->_value);
del = firstLeft;
if (parent->_left == firstLeft)
{
parent->_left = firstLeft->_right;
}
else
{
parent->_right = firstLeft->_right;
}
}
delete del;
return true;
}
}
return false;
}
Node* Find(const K& key) //非遞歸查找
{
if (_root == NULL)
{
return NULL;
}
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return NULL;
}
bool Insert_R(const K& key, const V& value) //遞歸實現插入
{
return _Insert_R(_root, key, value);
}
bool Remove_R(const K& key) //遞歸實現刪除
{
return _Remove_R(_root, key);
}
Node* Find_R(const K& key) //遞歸實現查找
{
return _Find_R(_root, key);
}
void Inorder() //遞歸實現中序遍歷
{
_Inorder(_root);
}
protected:
bool _Insert_R(Node*& root, const K& key, const V& value) //遞歸實現插入節點
{
if (root == NULL)
{
root = new Node(key, value); //添加引用會更改_root
return true;
}
if (root->_key < key)
{
return _Insert_R(root->_right, key, value);
}
else if (root->_key > key)
{
return _Insert_R(root->_left, key, value);
}
else
{
return false;
}
}
Node* _Find_R(Node*& root, const K& key) //遞歸實現查找
{
if (root == NULL)
{
return NULL;
}
if (root->_key < key)
{
return _Find_R(root->_right, key);
}
else if (root->_key > key)
{
return _Find_R(root->_left, key);
}
else
{
return root;
}
}
bool _Remove_R(Node*& root, const K& key)
{
if (root == NULL)
{
return false;
}
if (root->_key > key)
{
return _Remove_R(root->_left, key);
}
else if (root->_key < key)
{
return _Remove_R(root->_right, key);
}
else
{
Node* del = root;
if (root->_left == NULL)
{
root = root->_right;
delete del;
return true;
}
else if (root->_right == NULL)
{
root = root->_left;
delete del;
return true;
}
else
{
Node* firstLeft = root->_right;
while (firstLeft->_left)
{
firstLeft = firstLeft->_left;
}
swap(firstLeft->_key, root->_key);
swap(firstLeft->_value, root->_value);
_Remove_R(root->_right, key);
delete del;
return true;
}
}
return false;
}
void _Inorder(Node* root) //中序遍歷
{
if (root == NULL)
{
return;
}
_Inorder(root->_left);
cout << root->_key << " ";
_Inorder(root->_right);
}
protected:
Node* _root;
};另外有需要云服務器可以了解下創新互聯scvps.cn,海內外云服務器15元起步,三天無理由+7*72小時售后在線,公司持有idc許可證,提供“云服務器、裸金屬服務器、高防服務器、香港服務器、美國服務器、虛擬主機、免備案服務器”等云主機租用服務以及企業上云的綜合解決方案,具有“安全穩定、簡單易用、服務可用性高、性價比高”等特點與優勢,專為企業上云打造定制,能夠滿足用戶豐富、多元化的應用場景需求。
當前題目:數據結構--‘搜索二叉樹’-創新互聯
標題路徑:http://vcdvsql.cn/article26/cscjjg.html
成都網站建設公司_創新互聯,為您提供網站營銷、動態網站、關鍵詞優化、移動網站建設、品牌網站制作、云服務器
聲明:本網站發布的內容(圖片、視頻和文字)以用戶投稿、用戶轉載內容為主,如果涉及侵權請盡快告知,我們將會在第一時間刪除。文章觀點不代表本網站立場,如需處理請聯系客服。電話:028-86922220;郵箱:631063699@qq.com。內容未經允許不得轉載,或轉載時需注明來源: 創新互聯

- 響應式網站與移動版網站設計比較表 2019-01-18
- 響應式網站建設設計的關鍵點是什么? 2022-12-17
- 為何要做響應式網站設計 2023-01-21
- 為什么選擇響應式網站制作 2016-04-04
- 網站建設解決響應式網站圖片響應式難題 2016-04-27
- 南充響應式網站開發為什么越來越受歡迎 2013-07-03
- 響應式網站設計真的會成為未來趨勢嗎? 2022-11-30
- 響應式網站在高端定制下“大放異彩” 2021-04-22
- 響應式網站到底適不適合做維護? 2023-03-25
- 【成都網站建設】響應式網站在網絡運營的優勢 2022-12-10
- 響應式網站建設的重要性 2016-10-05
- 你知道做響應式網站的優勢嗎? 2022-07-20