小編給大家分享一下怎么使用Python實現(xiàn)正態(tài)分布、正態(tài)分布采樣，相信大部分人都還不怎么了解，因此分享這篇文章給大家參考一下，希望大家閱讀完這篇文章后大有收獲，下面讓我們一起去了解一下吧！

創(chuàng)新互聯(lián)專注于企業(yè)成都全網(wǎng)營銷推廣、網(wǎng)站重做改版、惠民網(wǎng)站定制設(shè)計、自適應(yīng)品牌網(wǎng)站建設(shè)、H5開發(fā)、商城網(wǎng)站定制開發(fā)、集團公司官網(wǎng)建設(shè)、成都外貿(mào)網(wǎng)站建設(shè)公司、高端網(wǎng)站制作、響應(yīng)式網(wǎng)頁設(shè)計等建站業(yè)務(wù)，價格優(yōu)惠性價比高，為惠民等各大城市提供網(wǎng)站開發(fā)制作服務(wù)。

多元正態(tài)分布(多元高斯分布)

直接從多元正態(tài)分布講起。多元正態(tài)分布公式如下：

這就是多元正態(tài)分布的定義，均值好理解，就是高斯分布的概率分布值大的位置，進行采樣時也就是采樣的中心點。而協(xié)方差矩陣在多維上形式較多。

協(xié)方差矩陣

一般來說，協(xié)方差矩陣有三種形式，分別稱為球形、對角和全協(xié)方差。以二元為例：

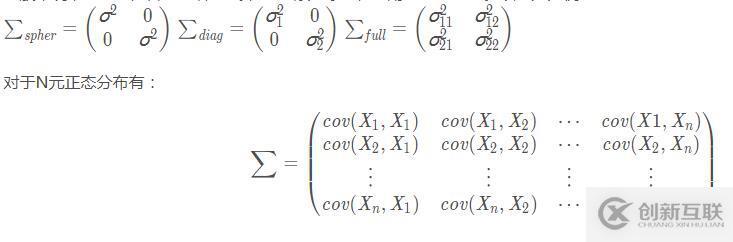
為了方便展示不同協(xié)方差矩陣的效果，我們以二維為例。(書上截的圖，湊活著看吧，是在不想畫圖了)

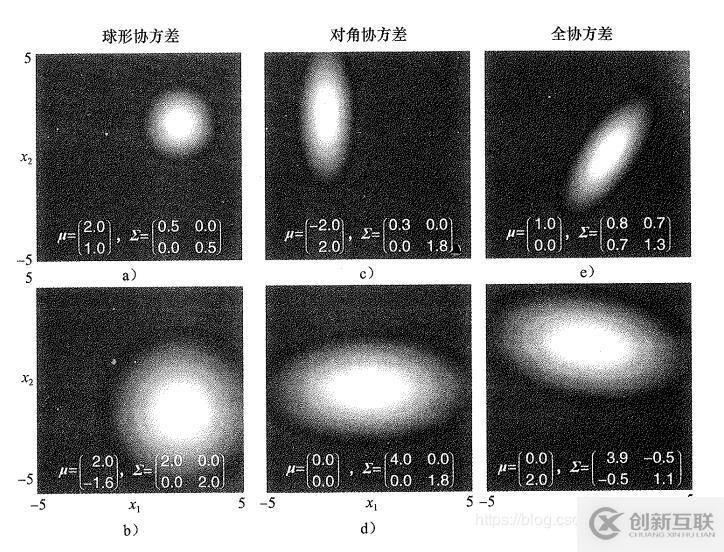
其實從這個圖上可以很好的看出，協(xié)方差矩陣對正態(tài)分布的影響，也就很好明白了這三個協(xié)方差矩陣是哪里來的名字了。可以看出，球形協(xié)方差矩陣，會產(chǎn)生圓形(二維)或者球形(三維)的等高線，對角協(xié)方差矩陣和全協(xié)方差矩陣，會產(chǎn)生橢圓形的等高線。更一般地，在一個D維空間中，球形協(xié)方差矩陣，會產(chǎn)生一個D維球面等高線；對角協(xié)方差矩陣，會產(chǎn)生一個坐標(biāo)軸對其的橢球型等高線；全協(xié)方差矩陣，會在任意位置產(chǎn)生一個坐標(biāo)軸對其的橢球型等高線。

當(dāng)協(xié)方差矩陣是球形的或者是對角的，單獨的變量之間是獨立的

協(xié)方差分解

時間不足，具體解釋以后再補

下面是協(xié)方差分解的原理圖

變量的線性變換(正態(tài)分布采樣原理)

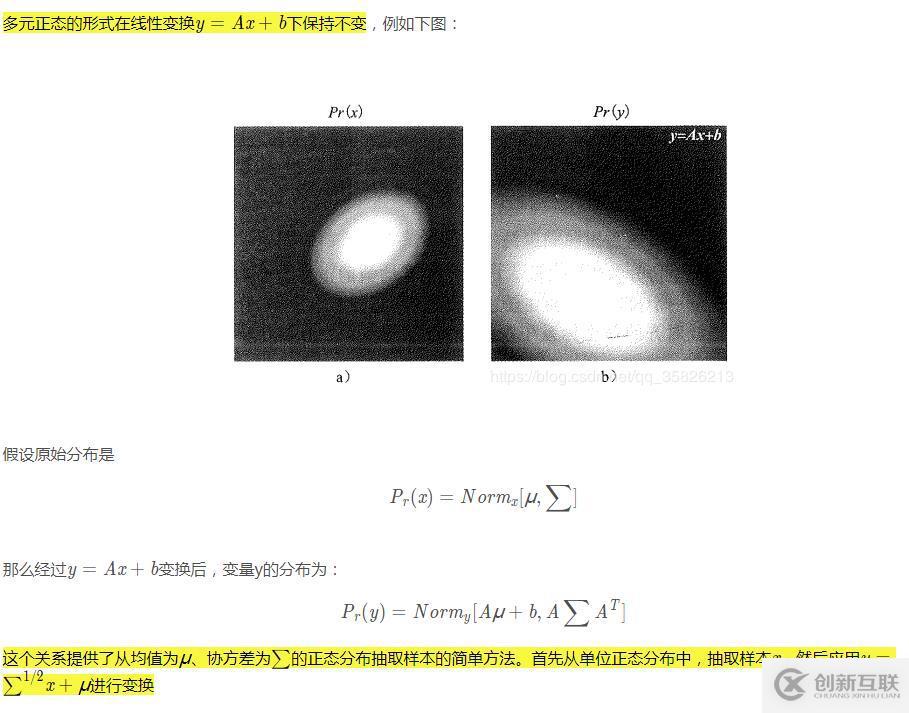
python實現(xiàn)

多元正態(tài)分布在python的numpy庫中有很方便一個函數(shù)：

np.random.multivariate_normal(mean=mean, cov=conv, size=N)

這個函數(shù)中，mean代表均值，是在每個維度中的均值。cov代表協(xié)方差矩陣，就像上面講的那種形式，協(xié)方差矩陣值的大小將決定采樣范圍的大小。size代表需要采樣生成的點數(shù)，此時輸出大小為（N*D）的坐標(biāo)矩陣。

另外，其他參數(shù)包括：check_valid，這個參數(shù)用于決定當(dāng)cov即協(xié)方差矩陣不是半正定矩陣時程序的處理方式，它一共有三個值：warn，raise以及ignore。當(dāng)使用warn作為傳入的參數(shù)時，如果cov不是半正定的程序會輸出警告但仍舊會得到結(jié)果；當(dāng)使用raise作為傳入的參數(shù)時，如果cov不是半正定的程序會報錯且不會計算出結(jié)果；當(dāng)使用ignore時忽略這個問題即無論cov是否為半正定的都會計算出結(jié)果

tol：檢查協(xié)方差矩陣奇異值時的公差，float類型。

下面是一個小demo

import numpy as np
import matplotlib.pyplot as plt

mean = np.array([2,1])    # 均值
conv = np.array([[0.5, 0.0],  # 協(xié)方差矩陣
     [0.0, 0.5]])
axis = np.random.multivariate_normal(mean=mean, cov=conv, size=200)
x, y = np.random.multivariate_normal(mean=mean, cov=conv, size=1000).T

# print(axis[:])

plt.plot(axis[:, 0], axis[:, 1], 'ro')
plt.show()
plt.plot(x, y, 'ro')
plt.show()

注意，單獨取出每個坐標(biāo)軸的坐標(biāo)數(shù)組時，需要在最后加上.T，否則會報錯 效果展示：

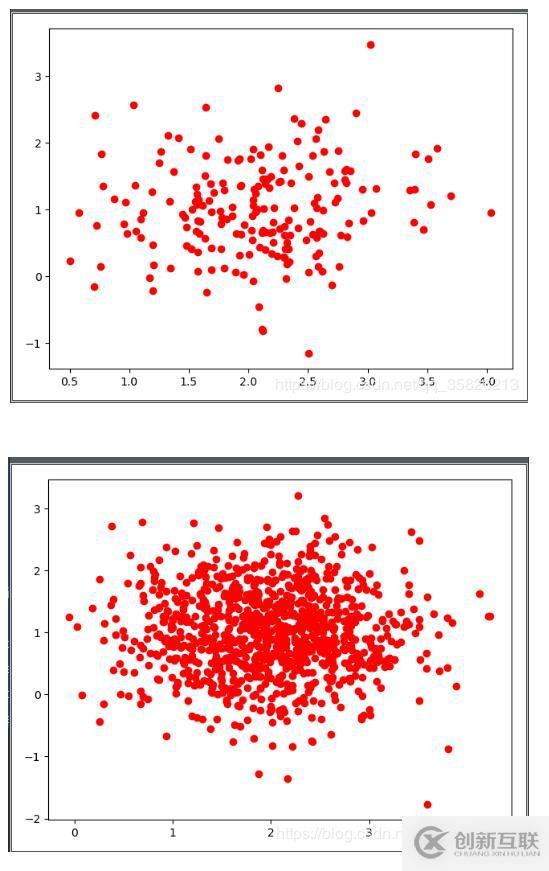
協(xié)方差值的大小對采樣的影響：

mean = np.array([2,1])    # 均值
conv = np.array([[0.5, 0.0],  # 協(xié)方差矩陣
     [0.0, 0.5]])

conv2 = np.array([[10, 0.0],  # 協(xié)方差矩陣
     [0.0, 10]])
axis = np.random.multivariate_normal(mean=mean, cov=conv, size=200)
x, y = np.random.multivariate_normal(mean=mean, cov=conv2, size=200).T

# print(axis[:])

plt.plot(axis[:, 0], axis[:, 1], 'ro')
plt.show()
plt.plot(x, y, 'ro')
plt.show()

效果如下：

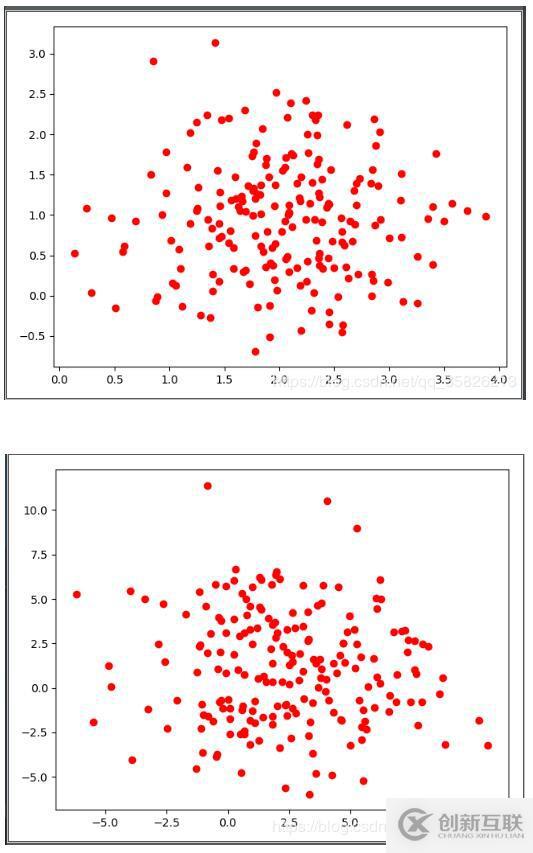
這里沒有設(shè)定隨機種子店，每次隨機數(shù)會有所不同。

以上是“怎么使用Python實現(xiàn)正態(tài)分布、正態(tài)分布采樣”這篇文章的所有內(nèi)容，感謝各位的閱讀！相信大家都有了一定的了解，希望分享的內(nèi)容對大家有所幫助，如果還想學(xué)習(xí)更多知識，歡迎關(guān)注創(chuàng)新互聯(lián)行業(yè)資訊頻道！

網(wǎng)站名稱：怎么使用Python實現(xiàn)正態(tài)分布、正態(tài)分布采樣-創(chuàng)新互聯(lián)
網(wǎng)頁地址：http://vcdvsql.cn/article30/ccchpo.html

成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián)，為您提供建站公司、虛擬主機、微信小程序、網(wǎng)站收錄、關(guān)鍵詞優(yōu)化、ChatGPT

廣告

聲明：本網(wǎng)站發(fā)布的內(nèi)容（圖片、視頻和文字）以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主，如果涉及侵權(quán)請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網(wǎng)站立場，如需處理請聯(lián)系客服。電話：028-86922220；郵箱：631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載，或轉(zhuǎn)載時需注明來源： 創(chuàng)新互聯(lián)