數據結構與算法，出發(fā)！

成都創(chuàng)新互聯(lián)公司成都網站建設按需網站制作，是成都網站建設公司,為紗窗提供網站建設服務,有成熟的網站定制合作流程，提供網站定制設計服務：原型圖制作、網站創(chuàng)意設計、前端HTML5制作、后臺程序開發(fā)等。成都網站改版熱線：028-86922220

數據結構與算法系列也將持續(xù)更新。

有C語言一定基礎的讀者可以來學習一下數據結構與算法~

如果對C語言還有遺憾或者是想再學習一下，請關注我的C語言初階系列

目錄

什么是數據結構？|? 什么是算法？

時間復雜度

嵌套循環(huán)時間復雜度的計算

雙重循環(huán)的時間復雜度的計算

常數循環(huán)的時間復雜度

strchar的時間復雜度

冒泡排序的時間復雜度

二分查找的時間復雜度

階乘遞歸的時間復雜度

斐波那契遞歸的時間復雜度

---

什么是數據結構？|? 什么是算法？

在很多地方，數據結構總是和算法放在一起叫的。

比如很多課程叫做《數據結構與算法》，而不是把它們分成獨立的課程。

在一些概念中，數據結構和算法被這樣定義：

數據結構是計算機存儲、組織數據的方式，指相互之間存在一定或多種數據元素的集合。

算法就是定義良好的計算過程，它取一個或一組的值為輸入，并產生一個或一組值作為輸出。簡單來說算法就是一系列的計算步驟，用來將輸入數據轉化成輸出結果。

看完這些概念，您理解嗎？

形象地來說，數據結構就是一些項目在實現(xiàn)的過程中，我們可能需要在內存中把數據給存儲起來。

比如說，要實現(xiàn)一個通訊錄，我們要把每個人的信息去存儲起來。

那怎么把它們存儲起來呢？

如果學習過C語言就知道要用數組存儲。

除了數組之外，還可以以鏈表、樹、哈希表的形式存儲......

不論是哪種形式，都有其特點。

用數組存儲，它的優(yōu)點就是很方便，缺點就是假如你數組有500個元素，那么存儲過500個人的信息后就不能再存儲了。

雖然C99標準可以使用動態(tài)數組，但還需要給數組擴容，比較麻煩。

而使用鏈表的話會更方便。只需要申請內存，然后用指針鏈接起來即可。

如果我們想去查找某個人，就可能要用到樹了。日后細講。

所以我們就要根據需求去選擇不同的數據結構，要去考慮用那種數據結構更合適。

算法有很多很多，如排序、查找、去重。

這些天手機圈有很多驚喜，榮耀發(fā)布了MgicOS、小米13對標iPhone等等......

如果我想買一部手機，想買最貴的，我就需要用價格去降序排序，想買最新發(fā)布的，就要根據時間去排序，想看一下大家買的比較多的，就要根據銷量去排序。

這就用到了排序算法。

還有很多很高級的算法，比如推薦算法。

刷短視頻，短視頻平臺會根據你的偏好去推薦相關的視頻。

數據結構和算法已經在日常生活中無處不在了。

要設計算法，很多時候就要用到數據結構。

數據結構和算法是不分家的，有些數據結構需要用到算法，有些算法需要用到數據結構。

什么是數據結構？什么是算法？筆者之所以把這兩個問題放在一塊，就是因為它們聯(lián)系太緊密了。

在C語言階段練習和總結并重，而在數據結構階段更側重好好寫代碼，還要學會畫圖和分析。

時間復雜度

算法分析分為兩個方面，一個是時間復雜度，另一個是空間復雜度。本節(jié)重點講解時間復雜度。

對于一個算法，我們要去判斷它的運行的好壞，最重要的是看它運行起來跑得快不快，除此之外還要看它占用多少空間。

時間復雜度主要衡量一個算法的運行快慢，空間復雜度主要衡量一個算法運行所需要的額外的空間。

早期的時候還比較關注空間，而現(xiàn)在基本上不關注空間了，因為現(xiàn)在內存越來越大了，能夠滿足內存占用較多的程序運行。

但是算法對時間還有一定的追求。

算法的時間復雜度是一個函數，但注意這里所指的函數是數學中的帶有未知數的函數表達式。

時間復雜度不去計算它能跑多少秒，因為一個程序在配置很低的機器上和配置很高的機器上的時間是不一樣的。

環(huán)境不同，具體運行時間不同。

算法中的基本操作的執(zhí)行次數，是算法的時間復雜度。

嵌套循環(huán)時間復雜度的計算

下面來計算下Func1基本操作執(zhí)行了多少次？

void Func1(int N)
{
    int count = 0;
    for (int i = 0; i< N; ++i)
    {
        for (int j = 0; j< N; ++j)
        {
            ++count;
        }
    }
    for (int k = 0; k< 2 * N; ++k)
    {
        ++count;
    }
    int M = 10;
    while (M--)
    {
        ++count;
    }
    printf("%d\n", count);
}

準確的次數是n^2+2n+10;

時間復雜度的函數式為

F(N)=N*N+2*N+10

我們看下這張圖：

如果我們把F(N)=N*N+2*N+10簡化一下，簡化成F(N)=N*N

那么

N=10時， 復雜度為100

N=100時，復雜度為10000

N=1000時，復雜度為1000000

可以發(fā)現(xiàn)，N越大，后兩項對結果的影響越小。

實際中我們計算時間復雜度時，我們其實并不一定要計算精確的執(zhí)行次數，而只需要大概執(zhí)行次數。

這就好比求極限，看下邊這道題：

當x趨于無窮大時，(x^2-1)/(2x^2-x-1)~1/2。

計算時間復雜度就好比求極限，在F(N)=N*N+2*N+10中，因為當N足夠大時，后邊式子對復雜度的影響越來越小，那我們就把它化簡成F(N)=N*N。

這里我們使用大O的漸進表示法。大O的漸進表示法就是估算。

大O符號（Big O notation）：是用于描述函數漸進行為的數學符號。

推導大O階方法：

1、用常數1取代運行時間中的所有加法常數。

2、在修改后的運行次數函數中，只保留最高階項。

3、如果最高階項存在且不是1，則去除與這個項目相乘的常數。得到的結果就是大O階。

那么就得出此算法的時間復雜度為O(N^2)。

雙重循環(huán)的時間復雜度的計算

請計算Func2的時間復雜度

void Func2(int N)
{
    int count = 0;
    for (int k = 0; k< 2 * N; ++k)
    {
        ++count;
    }
    int M = 10;
    while (M--)
    {
        ++count;
    }
    printf("%d\n", count);
}

精確的計算是2N+10。

那么當N無限大的時候，10對結果的影響很小。而當N無限大的時候N和2N是同一個級別。

在上文也提到如果最高階項存在且不是1，則去除與這個項目相乘的常數。

所以可得出O(N)。

再來一道題，請計算Func3的時間復雜度

void Func3(int N, int M)
{
    int count = 0;
    for (int k = 0; k< M; ++k)
    {
        ++count;
    }
    for (int k = 0; k< N; ++k)
    {
        ++count;
    }
    printf("%d\n", count);
}

結果為O(M+N)。

一般情況下計算時間復雜度都用N，但是也可以用M、K等等其他的。

M和N都是未知數，但是我們不知道是M大還是N大。

所以M和N都要用。

如果這道題有了條件：

如果條件是M遠大于N，那么結果為O(M)；

如果條件是N遠大于M，那么結果為O(N)；

如果條件是M和N差不多大，那么既可以用O(M)表示，也可以用O(N)表示。

常數循環(huán)的時間復雜度

請計算Func2的時間復雜度

void Func4(int N)
{
    int count = 0;
    for (int k = 0; k< 100; ++k)
    {
        ++count;
    }
    printf("%d\n", count);
}

這里沒有未知數，那就是100次。

根據推導大O階的方法用常數1取代運行時間中的所有加法常數，那么這道題的時間復雜度就是O(1)。

如果有人要求你把某個算法優(yōu)化到O(1)，這并不意味著只讓算法執(zhí)行一次，而是運行常數次。

strchar的時間復雜度

請計算strchar的時間復雜度：

const char* strchr(const char* str, int character);

這是一個庫函數，不怎么常用的庫函數，它的代碼大概如下：

while (*str)
{
    if (*str == character)
        return str;
    else
        ++str;
}

它的功能是在字符串里查找一個字符。

那么它的時間復雜度是多少？

假設我從“hello world”中查找字符：

假設我查找的是字符是h? ?----> ?O(1)

假設我查找的是字符是w? ?----> ?O(N/2)

假設我查找的是字符是d? ?----> ?O(N)

（我們不知道字符串的長度，那就用N。

那么這三種情況分別對應最好的情況、平均的情況、最壞的情況。

有些算法的時間復雜度存在最好、平均和最壞情況：

最好情況：任意輸入規(guī)模的最小運行次數(下界)

平均情況：任意輸入規(guī)模的期望運行次數

最壞情況：任意輸入規(guī)模的大運行次數(上界)

當一個算法隨著輸入不同，時間復雜度不同，時間復雜度做悲觀預期，看最壞情況。

我們一般最看重最壞的情況。只有極個別少數算法不需要考慮最壞和平均情況。

99%情況下都是看最壞情況！

冒泡排序的時間復雜度

請計算BubbleSort的時間復雜度：

void BubbleSort(int* a, int n)
{
    assert(a);
    for (size_t end = n; end >0; --end)
    {
        int exchange = 0;
        for (size_t i = 1; i< end; ++i)
        {
            if (a[i - 1] >a[i])
            {
                Swap(&a[i - 1], &a[i]);
                exchange = 1;
            }
        }
        if (exchange == 0)
            break;
    }
}

先算一個精確的，F(xiàn)(N)=(1+N)/2。

為什么是F(N)=(1+N)/2？

我們要去了解下冒泡排序的思想。有的算法不能只看代碼。

我們做最悲觀的考慮，那么每個數都參與了比較。

圖中紅色代表未比較過的數據，黃色方框代表已經排好序的數據，藍色線條代表比較次數。

從最右邊執(zhí)行過的次數可以發(fā)現(xiàn)，比較的總次數為(N-1)+(N-2)+(N-3)+···+1。

這是個等差數列，循環(huán)了N-1次，比較了(N-1)+(N-2)+(N-3)+···+1次。

也就是說項數為N-1，那么總次數為N*(N-1)/2。

它的時間復雜度為O(N^2)。

二分查找的時間復雜度

計算BinarySearch的時間復雜度：

int BinarySearch(int* a, int n, int x)
{
    assert(a);
    int begin = 0;
    int end = n - 1;
    while (begin< end)
    {
        int mid = begin + ((end - begin) >>1);
        if (a[mid]< x)
            begin = mid + 1;
        else if (a[mid] >x)
            end = mid;
        else
            return mid;
    }
    return -1;
}

算時間復雜度不能只去看幾層循環(huán)，而要去看他的思想。

如果只去看幾層循環(huán)，那么它的時間復雜度就是O(N)，然而這是錯的！

它的時間復雜度是O(log2N)。

關于二分查找的思想詳見我之前的博客http://t.csdn.cn/kIg93

二分查找最好的情況是O(1)，就是你要查找的數正好在中間。

事實上我們一般不關注最好情況，那么最壞情況是多少？

找不到是最壞的情況。

假設我們要查找X次也沒找到，那么2^X=N。

可知X=log2N

二分查找是一個非常厲害的算法。

在1000個數中查找，大概需要10次；

在100w個數中查找，大概需要20次；

在10億個數中查找，大概需要30次。

可以發(fā)現(xiàn)隨著N急劇增大，需要查找的次數變化并不是特別明顯。

用時間復雜度分析二分查找，才知道二分查找的神奇之處。

假設我們從14億人中找一個人，最多需要31次（前提是排好序了......）。

在有序的前提下，二分查找是一個很厲害的算法。

階乘遞歸的時間復雜度

計算階乘遞歸Fac的時間復雜度：

long long Fac(size_t N)
{
    if (0 == N)
        return 1;
    return Fac(N - 1) * N;
}

遞歸算法：遞歸次數*每次遞歸調用的次數。

遞歸次數好理解，那么每次遞歸調用的次數是什么？

比如if判斷是一次，然后return后邊的Fac里的計算是一次......但是這些都可以理解為常數次！

所以關注遞歸次數就好。

那么該算法的時間復雜度就是O(N)。

斐波那契遞歸的時間復雜度

計算斐波那契遞歸Fib的時間復雜度：

long long Fib(size_t)
{
    if (N< 3)
        return 1;
    return Fib(N - 1) + Fib(N - 2);
}

我們來看斐波那契遞歸的過程：

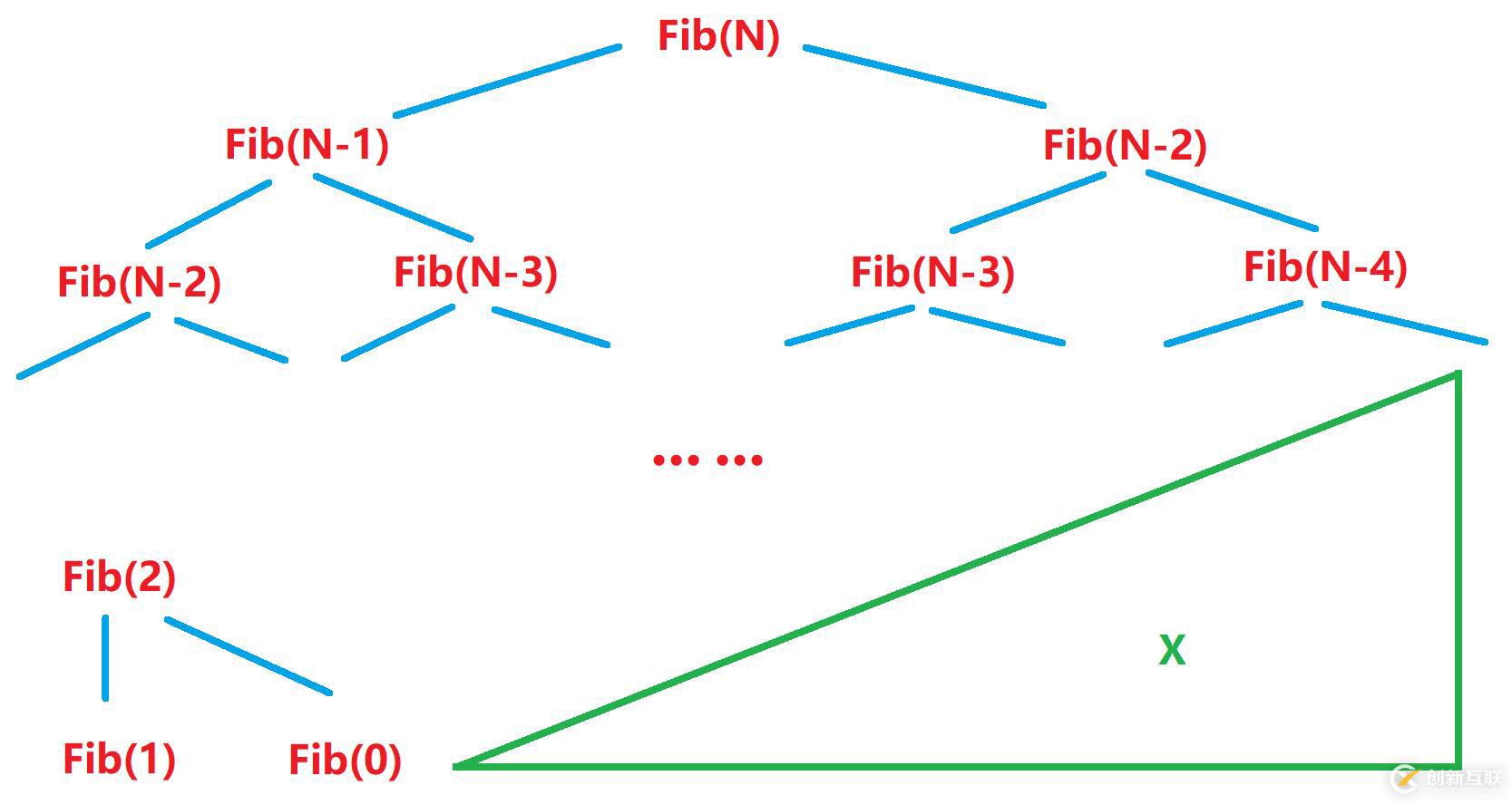
可以發(fā)現(xiàn)，右邊比左邊更早地完成了遞歸。

但是當N足夠大時，右邊比左邊少遞歸的次數X對整體遞歸次數的影響很小。

我們之前提到過：

遞歸算法：遞歸次數*每次遞歸調用的次數。

由于遞歸內調用次數可以理解為常數，那么

Fib(N)=2^0+2^1+2^3+······+2^(n-2)+2^(n-1)-X

不過X可以忽略不計，因為X前邊的次數和遠大于X。

那么用等比數列計算可得到

Fib(N)=2^N-1

1也可以忽略不計，所以時間復雜度為

O(2^N)

創(chuàng)作不易，這次碼了將近五千字，求各位老鐵三連支持下！

你是否還在尋找穩(wěn)定的海外服務器提供商？創(chuàng)新互聯(lián)www.cdcxhl.cn海外機房具備T級流量清洗系統(tǒng)配攻擊溯源，準確流量調度確保服務器高可用性，企業(yè)級服務器適合批量采購，新人活動首月15元起，快前往官網查看詳情吧

當前名稱：數據結構與算法-創(chuàng)新互聯(lián)
轉載注明：http://vcdvsql.cn/article32/epdsc.html

成都網站建設公司_創(chuàng)新互聯(lián)，為您提供搜索引擎優(yōu)化、品牌網站制作、關鍵詞優(yōu)化、移動網站建設、響應式網站、商城網站

廣告

聲明：本網站發(fā)布的內容（圖片、視頻和文字）以用戶投稿、用戶轉載內容為主，如果涉及侵權請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網站立場，如需處理請聯(lián)系客服。電話：028-86922220；郵箱：631063699@qq.com。內容未經允許不得轉載，或轉載時需注明來源： 創(chuàng)新互聯(lián)