本文小編為大家詳細(xì)介紹“Python如何實(shí)現(xiàn)線性規(guī)劃”，內(nèi)容詳細(xì)，步驟清晰，細(xì)節(jié)處理妥當(dāng)，希望這篇“Python如何實(shí)現(xiàn)線性規(guī)劃”文章能幫助大家解決疑惑，下面跟著小編的思路慢慢深入，一起來學(xué)習(xí)新知識吧。

成都網(wǎng)站建設(shè)哪家好，找創(chuàng)新互聯(lián)公司！專注于網(wǎng)頁設(shè)計(jì)、網(wǎng)站建設(shè)、微信開發(fā)、小程序制作、集團(tuán)企業(yè)網(wǎng)站制作等服務(wù)項(xiàng)目。核心團(tuán)隊(duì)均擁有互聯(lián)網(wǎng)行業(yè)多年經(jīng)驗(yàn)，服務(wù)眾多知名企業(yè)客戶；涵蓋的客戶類型包括：宣傳片制作等眾多領(lǐng)域，積累了大量豐富的經(jīng)驗(yàn)，同時(shí)也獲得了客戶的一致認(rèn)可！

 運(yùn)籌學(xué)

運(yùn)籌學(xué)是一種科學(xué)的決策方法，它通常是在需要分配稀缺資源的條件下，尋求系統(tǒng)的優(yōu)秀設(shè)計(jì)。科學(xué)的決策方法需要使用一個(gè)或多個(gè)數(shù)學(xué)模型(優(yōu)化模型)來做出最優(yōu)決策。

優(yōu)化模型試圖在滿足給定約束的決策變量的所有值的集合中，找到優(yōu)化(最大化或最小化)目標(biāo)函數(shù)的決策變量的值。 它的三個(gè)主要組成部分是：

1. 目標(biāo)函數(shù):要優(yōu)化的函數(shù)(最大化或最小化)。

2. 決策變量:影響系統(tǒng)性能的可控變量。

3. 約束:決策變量的一組約束(即線性不等式或等式)。非負(fù)性約束限制了決策變量取正值。

優(yōu)化模型的解稱為最優(yōu)可行解。

建模步驟

對運(yùn)籌學(xué)問題進(jìn)行準(zhǔn)確建模是很重要的任務(wù)，也是很困難的任務(wù)。錯(cuò)誤的模型會導(dǎo)致錯(cuò)誤的解決方案，從而不能解決原來的問題。團(tuán)隊(duì)成員應(yīng)按照以下步驟進(jìn)行建模：

1. 問題定義:定義項(xiàng)目的范圍，并確定三個(gè)要素:決策變量、目標(biāo)和限制(即約束)。

2. 模型構(gòu)建:將問題定義轉(zhuǎn)化為數(shù)學(xué)關(guān)系。

3. 模型求解:使用標(biāo)準(zhǔn)優(yōu)化算法。在獲得解后，需要進(jìn)行靈敏度分析，以找出由于某些參數(shù)的變化而導(dǎo)致的解的行為。

4. 模型有效性:檢查模型是否按預(yù)期工作。

5. 實(shí)現(xiàn):將模型和結(jié)果轉(zhuǎn)換為解決方案。

線性規(guī)劃

線性規(guī)劃(Linear  Programming，也稱為LP)是一種運(yùn)籌學(xué)技術(shù)，當(dāng)當(dāng)所有的目標(biāo)和約束都是線性的(在變量中)并且當(dāng)所有的決策變量都是連續(xù)的時(shí)使用。線性規(guī)劃是最簡單的運(yùn)籌學(xué)方法。

Python的SciPy庫包含用于解決線性編程問題的linprog函數(shù)。在使用linprog時(shí)，編寫代碼要考慮的兩個(gè)注意事項(xiàng)：

1. 這個(gè)問題必須表述為一個(gè)最小化問題。

2. 不等式必須表示為≤。

最小化問題

讓我們考慮以下要解決的最小化問題：

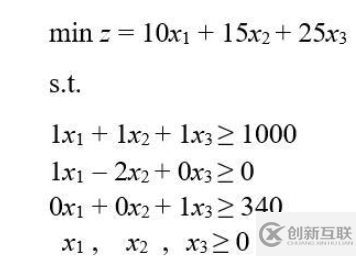
讓我們看一下Python代碼：

# Import required libraries import numpy as np from scipy.optimize import linprog  # Set the inequality constraints matrix # Note: the inequality constraints must be in the form of <= A = np.array([[-1, -1, -1], [-1, 2, 0], [0, 0, -1], [-1, 0, 0], [0, -1, 0], [0, 0, -1]])  # Set the inequality constraints vector b = np.array([-1000, 0, -340, 0, 0, 0])  # Set the coefficients of the linear objective function vector c = np.array([10, 15, 25])  # Solve linear programming problem res = linprog(c, A_ub=A, b_ub=b)  # Print results print('Optimal value:', round(res.fun, ndigits=2),       '\nx values:', res.x,       '\nNumber of iterations performed:', res.nit,       '\nStatus:', res.message)

輸出結(jié)果：

# Optimal value: 15100.0  # x values: [6.59999996e+02 1.00009440e-07 3.40000000e+02]  # Number of iterations performed: 7  # Status: Optimization terminated successfully.

最大化問題

由于Python的SciPy庫中的linprog函數(shù)是用來解決最小化問題的，因此有必要對原始目標(biāo)函數(shù)進(jìn)行轉(zhuǎn)換。通過將目標(biāo)函數(shù)的系數(shù)乘以-1(即通過改變其符號)，可以將最小化問題轉(zhuǎn)化為一個(gè)最大化問題。

讓我們考慮下面需要解決的最大化問題:

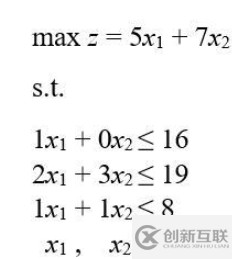
讓我們看一下Python的實(shí)現(xiàn)：

# Import required libraries import numpy as np from scipy.optimize import linprog  # Set the inequality constraints matrix # Note: the inequality constraints must be in the form of <= A = np.array([[1, 0], [2, 3], [1, 1], [-1, 0], [0, -1]])  # Set the inequality constraints vector b = np.array([16, 19, 8, 0, 0])  # Set the coefficients of the linear objective function vector # Note: when maximizing, change the signs of the c vector coefficient c = np.array([-5, -7])  # Solve linear programming problem res = linprog(c, A_ub=A, b_ub=b)  # Print results print('Optimal value:', round(res.fun*-1, ndigits=2),       '\nx values:', res.x,       '\nNumber of iterations performed:', res.nit,       '\nStatus:', res.message)

上述代碼的輸出結(jié)果為：

# Optimal value: 46.0  # x values: [5. 3.]  # Number of iterations performed: 5  # Status: Optimization terminated successfully.

讀到這里，這篇“Python如何實(shí)現(xiàn)線性規(guī)劃”文章已經(jīng)介紹完畢，想要掌握這篇文章的知識點(diǎn)還需要大家自己動手實(shí)踐使用過才能領(lǐng)會，如果想了解更多相關(guān)內(nèi)容的文章，歡迎關(guān)注創(chuàng)新互聯(lián)行業(yè)資訊頻道。

標(biāo)題名稱：Python如何實(shí)現(xiàn)線性規(guī)劃
URL標(biāo)題：http://vcdvsql.cn/article32/gjeesc.html

成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián)，為您提供虛擬主機(jī)、網(wǎng)站收錄、網(wǎng)站導(dǎo)航、網(wǎng)站設(shè)計(jì)公司、自適應(yīng)網(wǎng)站、做網(wǎng)站

廣告

聲明：本網(wǎng)站發(fā)布的內(nèi)容（圖片、視頻和文字）以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主，如果涉及侵權(quán)請盡快告知，我們將會在第一時(shí)間刪除。文章觀點(diǎn)不代表本網(wǎng)站立場，如需處理請聯(lián)系客服。電話：028-86922220；郵箱：631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載，或轉(zhuǎn)載時(shí)需注明來源： 創(chuàng)新互聯(lián)