建堆的方式、堆排序以及TopK問題

• 1、建堆的兩種方式
• • 1.1 向上調整建堆
  • 1.2 向下調整建堆
• 2、堆排序
• 3、TopK問題
• 4、建堆、堆排序、TopK問題全部代碼

超過10多年行業經驗，技術領先，服務至上的經營模式，全靠網絡和口碑獲得客戶，為自己降低成本，也就是為客戶降低成本。到目前業務范圍包括了：成都網站建設、成都網站設計，成都網站推廣，成都網站優化，整體網絡托管，微信平臺小程序開發，微信開發，重慶APP開發公司，同時也可以讓客戶的網站和網絡營銷和我們一樣獲得訂單和生意！1、建堆的兩種方式

我們知道，堆是二叉樹的一種，二叉樹的建立是借助結構體與數組完成的（通過在結構體中創建動態開辟的數組變量儲存堆中的元素）。
除了借助結構體外，有沒有其他方式，直接建堆。

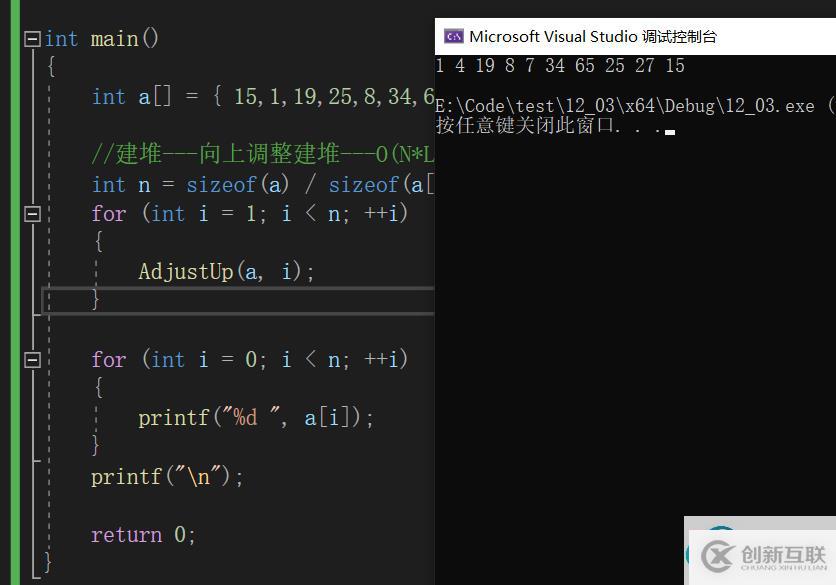
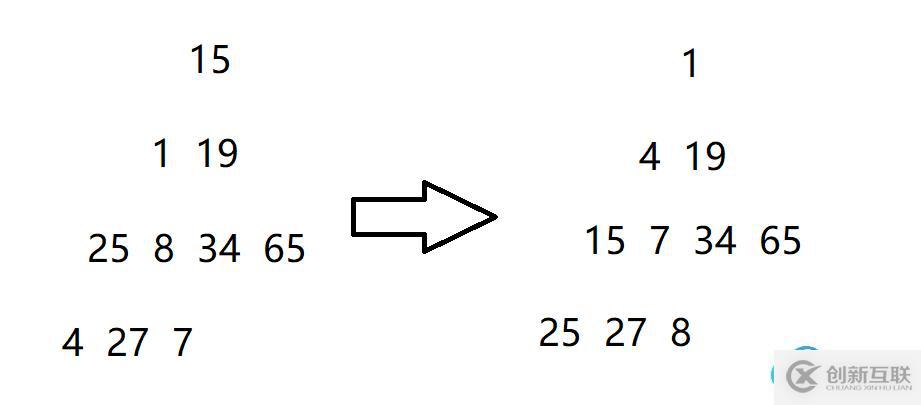
1.1 向上調整建堆

//交換函數
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

//向上調整函數
typedef int HPDataType;
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;  //找到堆最后一個數的父親的下標
	while (child >0)   //孩子的下標等于0時，說明堆從最后一個數一路向上比較，已經到達堆頂了
	{//小根堆，任意孩子的值要大于父節點的值，不是的話則要向上調整
		if (a[child]< a[parent])   //改為>，這個堆結構就成為大堆了
		{	Swap(&a[child], &a[parent]);

			//修正父親與孩子的下標，通過循環不斷比較，直到成為堆的形狀
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{	break;
		}
	}
}

int main()
{int a[] = {15,1,19,25,8,34,65,4,27,7 };

   //建堆---向上調整建堆---O(N*LogN)
	int n = sizeof(a) / sizeof(a[0]);
	for (int i = 1; i< n; ++i)
	{AdjustUp(a, i);
	}

	for (int i = 0; i< n; ++i)
	{printf("%d ", a[i]);
	}
	printf("\n");

	return 0;
}

打印結果


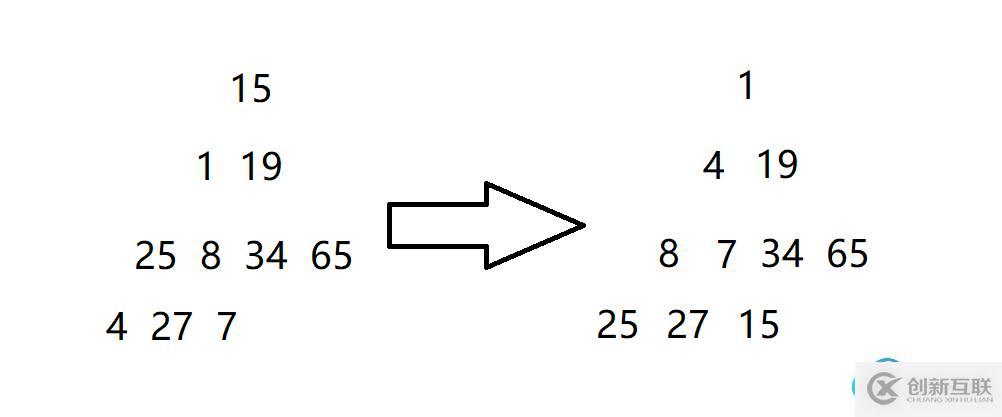
1.打印結果將一串無序的數組建立成為小堆。只要將向上調整中的if語句中的小于符號改成大于符號，建成的就是大堆。
2.向上調整建堆從第二個節點開始向上調整（即數組下標為1的節點），因為第一個節點是根節點，根節點沒有父節點，再往上就沒有節點了。第二個節點向上調整完畢，接著第三個節點，然后第四個節點、第五個節點，直到最后一個節點向上調整完畢。
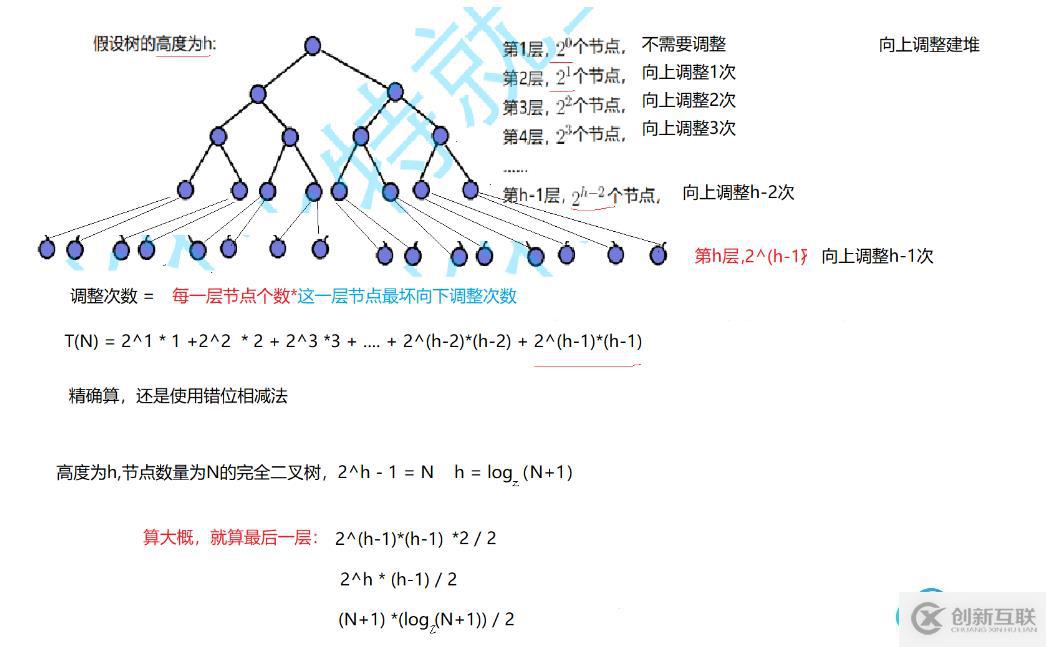
3.向上調整建堆的時間復雜度

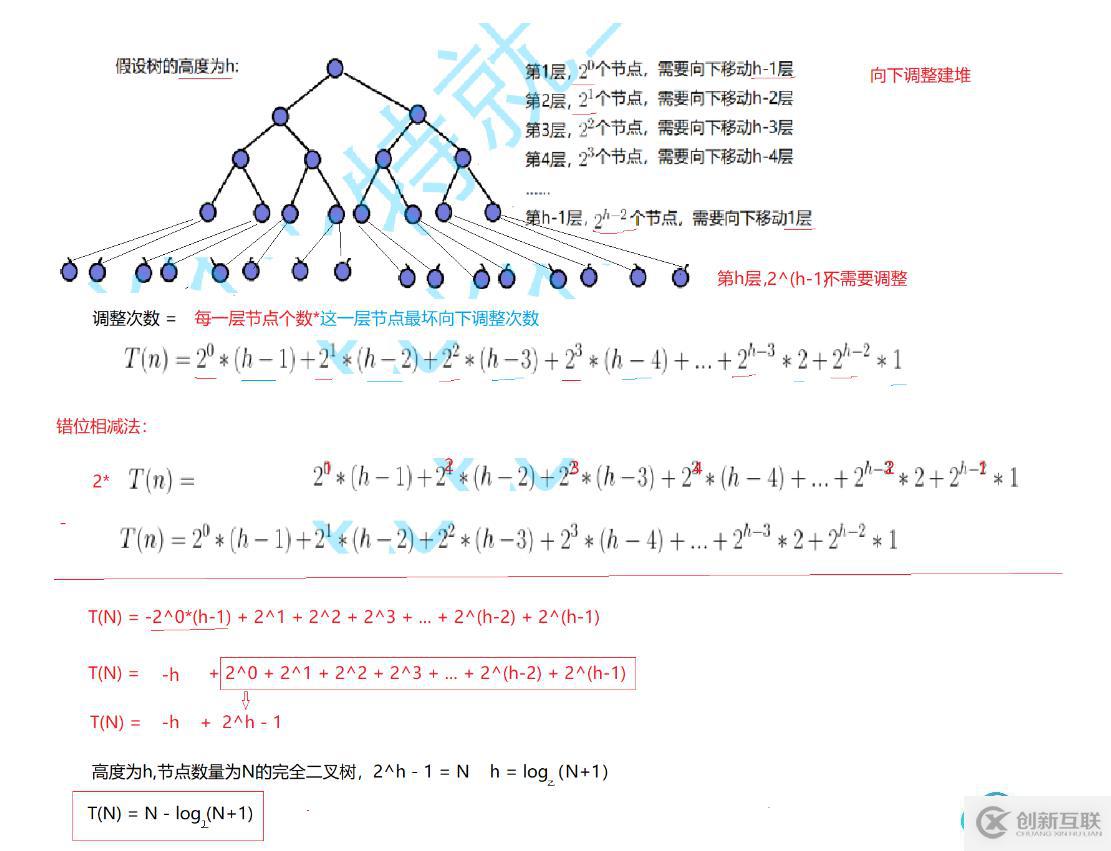
可以看到，在一棵樹中，越往下的節點，向上調整的次數越多，并且越往下的層級包含的節點數越多，所以越往下的層級每個節點向上調整的次數加起來是越大的。由上述式子計算，最后一層所有節點總共需要向上調整的次數大為(N+1) * ((log(N+1)-1)/2)，即最后一層需要向上調整的時間復雜度為O(N * log(N))。因為最后一層的時間復雜度已經是大的，前面所有層級加起來的時間復雜度也不會超過，所以向上調整總的時間復雜度為O(N * log(N))。

1.2 向下調整建堆

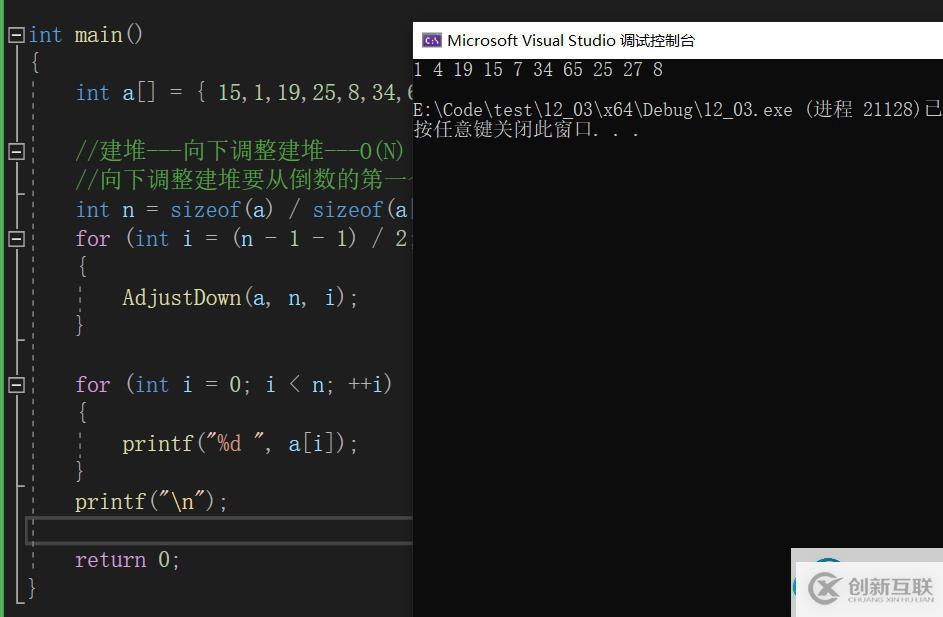
//交換函數
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

//向下調整函數
typedef int HPDataType;
void AdjustDown(HPDataType* a, int n, int parent)
{int minChild = parent * 2 + 1; //先默認左邊的孩子是整個小根堆中次小的孩子
	while (minChild< n)
	{//與右孩子比較一下，找出小的那個孩子的下標
		if (minChild + 1< n && a[minChild + 1]< a[minChild])
		{	minChild++;
		}
		//找到次小的孩子后將其與父節點比較
		if (a[minChild]< a[parent])
		{	Swap(&a[minChild], &a[parent]);
			//修正父親與孩子的下標，通過循環不斷比較，直到成為堆的形狀
			parent = minChild;
			minChild = parent * 2 + 1;
		}
		else
		{	break;
		}
	}

}

int main()
{int a[] = {15,1,19,25,8,34,65,4,27,7 };

	//建堆---向下調整建堆---O(N)
	//向下調整建堆要從倒數的第一個非葉子節點開始向下調整，一直調整到根節點位置
	int n = sizeof(a) / sizeof(a[0]);
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{AdjustDown(a, n, i);
	}

	for (int i = 0; i< n; ++i)
	{printf("%d ", a[i]);
	}
	printf("\n");

	return 0;
}

打印結果


1.打印結果將一串無序的數組建立成為小堆。只要將向下調整中的兩個if語句中的小于符號改成大于符號，建成的就是大堆。
2.向下調整建堆從倒數的第一個非葉子節點開始向下調整，因為葉子節點往下沒有子節點了，不用在往下調整了。倒數第一個非葉子節點調整完畢，接著倒數第二個非葉子節點向下調整，然后倒數第三個非葉子節點向下調整，一直到根節點位置向下調整。(n-1-1)/2 是在找倒數第一個非葉子節點。
3.向下調整時間復雜度

由上述式子算出，向下調整建堆最壞需要向下調整N-log(N+1)次，因此向下調整建堆的時間復雜度為O(N)。

總結： 經由上述可知，向下調整建堆的時間復雜度與向上調整建堆的時間復雜度相比，向下調整建堆所需時間更少，因此在沒有結構體構造堆的情況下，選擇向下調整直接建堆。

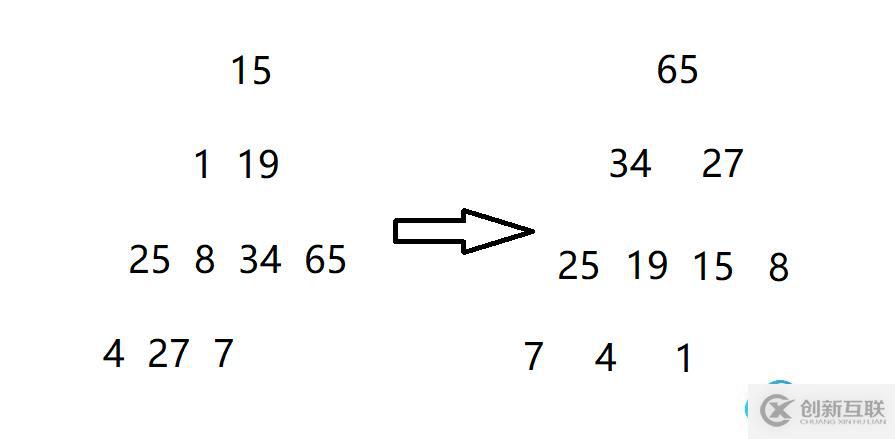
2、堆排序

void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

//向下調整函數
typedef int HPDataType;
void AdjustDown(HPDataType* a, int n, int parent)
{int minChild = parent * 2 + 1; //先默認左邊的孩子是整個小根堆中次小的孩子
	while (minChild< n)
	{//與右孩子比較一下，找出小的那個孩子的下標
		if (minChild + 1< n && a[minChild + 1]< a[minChild])
		{	minChild++;
		}
		//找到次小的孩子后將其與父節點比較
		if (a[minChild]< a[parent])
		{	Swap(&a[minChild], &a[parent]);
			//修正父親與孩子的下標，通過循環不斷比較，直到成為堆的形狀
			parent = minChild;
			minChild = parent * 2 + 1;
		}
		else
		{	break;
		}
	}

}

//堆排序函數
//大思路：選擇排序，依次選數，從后往前排
//升序---先建大堆，建堆完畢后，此時大的數在第一位，把第一個和最后一個的位置進行交換，
// 交換完畢后，把最后一個不看做堆里面的，進行向下調整，選出次大的。后續依次類似處理。

//降序---先建小堆，建堆完畢后，此時最小的數在第一位，把第一個和最后一個的位置進行交換，
//交換完畢后，把最后一個不看做堆里面的，進行向下調整，選出次小的。后續依次類似處理。
void HeapSort(int* a, int n)
{//建堆---向下調整建堆---O(N)
	//向下調整建堆要從倒數的第一個非葉子節點開始向下調整，一直調整到根節點位置
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{AdjustDown(a, n, i);
	}

	//選數
	int i = 1;
	while (i< n)
	{Swap(&a[0], &a[n - i]);  //交換第一個數跟最后一個數
		AdjustDown(a, n - i, 0);
		++i;
	}
}

int main()
{int a[] = {15,1,19,25,8,34,65,4,27,7 };
	HeapSort(a, sizeof(a) / sizeof(int));

	for (size_t i = 0; i< sizeof(a) / sizeof(int); ++i)
	{printf("%d ", a[i]);
	}
	printf("\n");

	return 0;
}

打印結果


1.打印結果將一串無序的數組建立成為降序的小堆。
2.堆排序的思路：
大思路：選擇排序，依次選數，從后往前排

2.1升序—先建大堆，建堆完畢后，此時大的數在第一位，把第一個和最后一個的位置進行交換，
交換完畢后，把最后一個不看做堆里面的，進行向下調整，選出次大的。后續依次類似處理。
2.2降序—先建小堆，建堆完畢后，此時最小的數在第一位，把第一個和最后一個的位置進行交換，
交換完畢后，把最后一個不看做堆里面的，進行向下調整，選出次小的。后續依次類似處理。

3、TopK問題

TopK問題就是在N個數中選出大的前K個數或者最小的前K個數來。
這個問題有兩種思路，例如選出大的前K個數，
思路1，建大堆（用向下調整建堆的方式），將根節點與尾節點進行交換(此時根節點上的數為大的數)，交換后不將尾節點算入堆中，剩余的N-1個數重新建堆，重復K次，這樣大的前K個數就被篩選出來了。
時間復雜度為O(N+(logN)* K)。
思路2，建小堆（用向下調整建堆的方式），用N個數中的前K個數建一個K個數的小堆，剩余的N-K個數一一與堆頂比較，只要比堆頂大就入隊，入堆后再重新向下調整建成小堆。當比較完畢后，小堆中的K個數就是在N個數中選出的大前K個數。時間復雜度為K+(log(k)) *(N-K)。

分析思路1與思路2的優劣： 當N很大，K很小的時候，選第二種方式，例如當N=100億，K=100，100億個整數有400億個字節(Byte)，一個G有1024 *1024 *1024(Byte)=1073741824個字節(Byte)≈1000000000=10億字節(Byte)，所以當N=100億時，要占用的空間為400÷10=40個G，所占內存過大，所以一般選用思路2的方式，即：
在N個數中選出大的前K個數-----建小堆
在N個數中選出最小的前K個數-----建大堆

在文件中先寫入10個數，選取這十個數中大的前3個數，代碼如下：

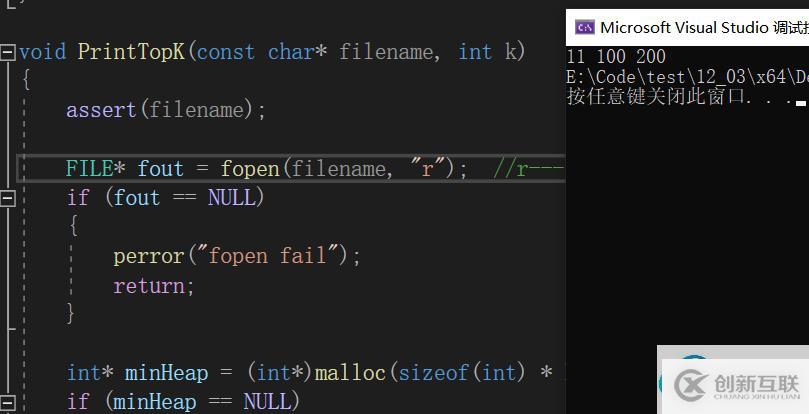
void PrintTopK(const char* filename, int k)
{assert(filename);

	FILE* fout = fopen(filename, "r");   //r--->在Test,c這個源文件路徑下打開一個本身已經存在的叫Data.txt的文件，將這個文件的地址賦值給文件指針
	if (fout == NULL)
	{perror("fopen fail");
		return;
	}

	int* minHeap = (int*)malloc(sizeof(int) * k);
	if (minHeap == NULL)
	{perror("malloc fail");
		return;
	}
	//如何讀取前k個數
	for (int i = 0; i< k; ++i)
	{fscanf(fout, "%d", &minHeap[i]);
	}

	//建堆,將讀取的前k個數建成小堆，向下調整建堆
	for (int j = (k - 1 - 1) / 2; j >= 0; --j)
	{AdjustDown(minHeap, k, j);
	}
	//繼續讀取N-k個數
	int val = 0;
	while (fscanf(fout, "%d", &val) != EOF)
	{if (val >minHeap[0])
		{	minHeap[0] = val;
			AdjustDown(minHeap, k, 0);
		}
	}

	for (int i = 0; i< k; ++i)
	{printf("%d ", minHeap[i]);
	}

	free(minHeap);
	fclose(fout);
}

//top k問題  N個數，找出這N個數中大的前k個數
int main()
{const char* filename = "Data.txt";
	int k = 3;
	PrintTopK(filename, k);

	return 0;
}

1.Fopen：打開文件，Fclose：關閉文件，fscanf：從文件中讀取數據(即從文件中輸入數據到屏幕上，sanf是從鍵盤上輸入數據到屏幕上)
2.fscanf(fout, “%d”, &val)；從fout中以 %d的類型讀取數據到變量val中。
3.已經存在的data.txt文件中10個數為 0 3 11 2 4 1 100 2 200 5。文件放在與Tsetc同一級的目錄下。
4.打印結果為

前3個大的數被選出來了，被選出來的數并不是有序的，這里有序只不過是巧合而已。
5. 向下調整函數的實現被寫在了Heap.c中，在第一節中，向下調整的實現已經寫過了，這里就不搬上來了。

在文件中隨機生成10000個數（1~10000中的任意數，包含了重復的數），選出其中大的前10個數來，如何實現？
這個只要多寫一個在文件中隨機生成數的函數就行，代碼如下。

//在文件中隨機數的生成
void CreateDataFile(const char* filename, int k)
{assert(filename);
	FILE* fin = fopen(filename, "w"); //w--->在test.c這個源文件路徑下創建一個test.txt的文件，如果這個文件已經存在，則將
	                                  //這個文件里的內容全部銷毀，相當于重新創建了這個文件。
	if (fin == NULL)
	{perror("fin fail");
		return;
	}
	srand(time(0));
	for (int i = 0; i< k; ++i)
	{fprintf(fin, "%d\n", rand()%10000);
	}

	fclose(fin);
}

void PrintTopK(const char* filename, int k)
{assert(filename);

	FILE* fout = fopen(filename, "r");  //r--->在Test,c這個源文件路徑下打開一個本身已經存在的叫Data.txt的文件，將這個文件的地址賦值給文件指針
	if (fout == NULL)
	{perror("fopen fail");
		return;
	}

	int* minHeap = (int*)malloc(sizeof(int) * k);
	if (minHeap == NULL)
	{perror("malloc fail");
		return;
	}
	//如何讀取前k個數
	for (int i = 0; i< k; ++i)
	{fscanf(fout, "%d", &minHeap[i]);
	}

	//建堆,將讀取的前k個數建成小堆
	for (int j = (k - 1 - 1) / 2; j >= 0; --j)
	{AdjustDown(minHeap, k, j);
	}
	//繼續讀取N-k個數
	int val = 0;
	while (fscanf(fout, "%d", &val) != EOF)
	{if (val >minHeap[0])
		{	minHeap[0] = val;
			AdjustDown(minHeap, k, 0);
		}
	}

	for (int i = 0; i< k; ++i)
	{printf("%d ", minHeap[i]);
	}

	free(minHeap);
	fclose(fout);
}

int main()
{const char* filename = "Data.txt";
	int N = 10000;
	int k = 10;

	CreateDataFile(filename, N);
	PrintTopK(filename, k);
	
	return 0;
}

1.void CreateDataFile(const char* filename, int k);---->在文件中生成隨機數
2.如何生成隨機數?
rand()函數能夠生成不同的偽隨機數，如果要生成0到10000之間的偽隨機數，則rand()%10000，這樣生成的偽隨機數就是0~9999。不過如果直接使用rand(),每次生成的偽隨機數都是一樣的，比如第一次生成的是1 4 99 3……，下一次運行程序生成的還是1 4 99 3……，因此每次使用rand()前都要先使用srand()初始化一遍，如果srand()中的參數是固定的話，每次初始化的值也是一樣的，即每次調用rand()生成的偽隨機數還是一樣的，因此需要srand()中的參數不是固定的，這樣每次調用rand()時，生成的偽隨機數才能不是一樣的。剛好，電腦上流動的時間是在變化的，運用時間戳函數time(),能夠將每時每刻的時間轉換為time_t類型的值，不同時間調用time()，生成的值都不同，因此這個值作為srand()的參數，隨著srand()中的參數變化，每次初始化的值也不一樣了，rand()生成的偽隨機數也不一樣了。
time()的頭文件是time.h
3.fprintf(fin, “%d\n”, rand()%10000)；—>將參數3以%d的類型寫進文件指針fin指向的文件。
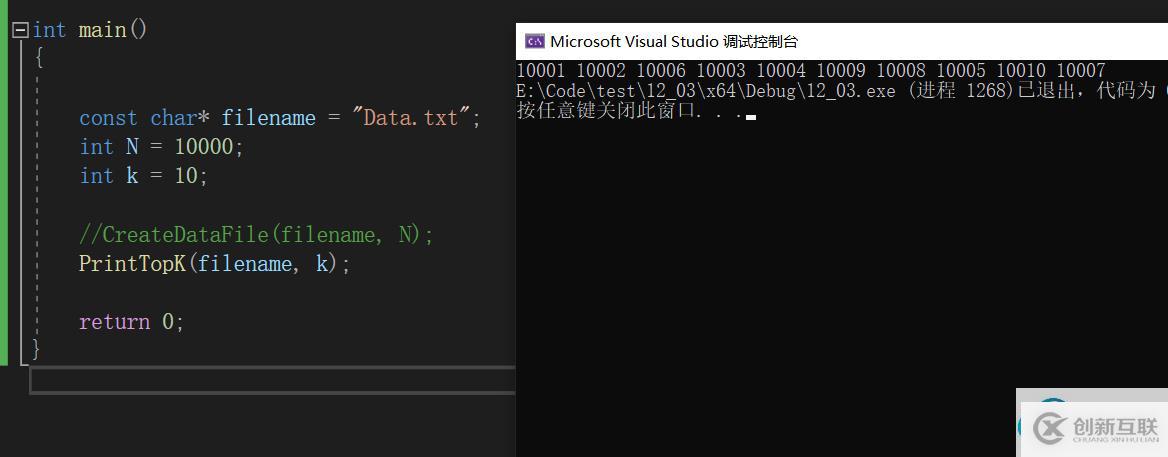
打印結果


上述文本文件是在文件中隨機生成的1000個數中截取的一部份，運行結果是這一萬個數種大的前十個數。因為隨機生成的數有重復的，因此大的前十個數也有重復的。
4.如何驗證這個程序的正確性？
答：首相將隨機生成數函數屏蔽，然后在之前已經生成的隨機數種中手動加入十個比這一萬個數都大的數，如果程序運行后，能把這手動添加的數全部選出來，說明程序無誤。現在加入 10001 10002 10003……10010。

int main()
{const char* filename = "Data.txt";
	int N = 10000;
	int k = 10;

	//CreateDataFile(filename, N);
	PrintTopK(filename, k);

	return 0;
}

打印結果

手動加入的十個大的數全部被挑選出來，說明程序無誤。

4、建堆、堆排序、TopK問題全部代碼

Heap.h部分：寫函數的聲明，函數的頭文件。

#pragma once

#include#include 
#include#include#include//堆是完全二叉樹
//堆的二叉樹用數組表示，在數組的順序從上至下，從左至右
//小根堆，任何節點的值小于等于孩子的值
//大根堆，任何節點的值大于等于孩子的值
//數組下標計算父子關系的公式
//leftchild = parent*2 + 1   左孩子的數組下標都是奇數
//rightchild = parent*2 + 2  右孩子的數組下標都是偶數
//parent = (child - 1)/2


typedef int HPDataType;

//向上調整
void AdjustUp(HPDataType* a, int child);

//向下調整
void AdjustDown(HPDataType* a, int n, int parent);

//交換函數
void Swap(HPDataType* p1, HPDataType* p2);

//在文件中隨機數的生成
void CreateDataFile(const char* filename, int k);

//TopK函數
void PrintTopK(const char* filename, int k);

Heap.c部分：各自定義函數的實現

#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"

void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}


//向上調整函數
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;  //找到堆最后一個數的父親的下標
	while (child >0)   //孩子的下標等于0時，說明堆從最后一個數一路向上比較，已經到達堆頂了
	{//小根堆，任意孩子的值要大于父節點的值，不是的話則要向上調整
		if (a[child]< a[parent])   //改為>，這個堆結構就成為大堆了
		{	Swap(&a[child], &a[parent]);

			//修正父親與孩子的下標，通過循環不斷比較，直到成為堆的形狀
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{	break;
		}
	}
}


//向下調整函數
void AdjustDown(HPDataType* a, int n, int parent)
{int minChild = parent * 2 + 1; //先默認左邊的孩子是整個小根堆中次小的孩子
	while (minChild< n)
	{//與右孩子比較一下，找出小的那個孩子的下標
		if (minChild + 1< n && a[minChild + 1]< a[minChild])
		{	minChild++;
		}
		//找到次小的孩子后將其與父節點比較
		if (a[minChild]< a[parent])
		{	Swap(&a[minChild], &a[parent]);
			//修正父親與孩子的下標，通過循環不斷比較，直到成為堆的形狀
			parent = minChild;
			minChild = parent * 2 + 1;
		}
		else
		{	break;
		}
	}

}


//在文件中隨機數的生成
void CreateDataFile(const char* filename, int k)
{assert(filename);
	FILE* fin = fopen(filename, "w"); //w--->在test.c這個源文件路徑下創建一個test.txt的文件，如果這個文件已經存在，則將
	//這個文件里的內容全部銷毀，相當于重新創建了這個文件。
	if (fin == NULL)
	{perror("fin fail");
		return;
	}
	srand(time(0));
	for (int i = 0; i< k; ++i)
	{fprintf(fin, "%d\n", rand() % 10000);
	}

	fclose(fin);
}


//TopK函數
void PrintTopK(const char* filename, int k)
{assert(filename);

	FILE* fout = fopen(filename, "r");  //r--->在Test,c這個源文件路徑下打開一個本身已經存在的叫Data.txt的文件，將這個文件的地址賦值給文件指針
	if (fout == NULL)
	{perror("fopen fail");
		return;
	}

	int* minHeap = (int*)malloc(sizeof(int) * k);
	if (minHeap == NULL)
	{perror("malloc fail");
		return;
	}
	//如何讀取前k個數
	for (int i = 0; i< k; ++i)
	{fscanf(fout, "%d", &minHeap[i]);
	}

	//建堆,將讀取的前k個數建成小堆
	for (int j = (k - 1 - 1) / 2; j >= 0; --j)
	{AdjustDown(minHeap, k, j);
	}
	//繼續讀取N-k個數
	int val = 0;
	while (fscanf(fout, "%d", &val) != EOF)
	{if (val >minHeap[0])
		{	minHeap[0] = val;
			AdjustDown(minHeap, k, 0);
		}
	}

	for (int i = 0; i< k; ++i)
	{printf("%d ", minHeap[i]);
	}

	free(minHeap);
	fclose(fout);
}

Test.c部分：主函數放在這，在主函數中調用各自定義函數。在實現各函數時，可以用來測試各函數的功能。

#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"

//向上調整建堆
int main()
{int a[] = {15,1,19,25,8,34,65,4,27,7 };

    //建堆---向上調整建堆---O(N*LogN)
	int n = sizeof(a) / sizeof(a[0]);
	for (int i = 1; i< n; ++i)
	{AdjustUp(a, i);
	}

	for (int i = 0; i< n; ++i)
	{printf("%d ", a[i]);
	}
	printf("\n");

	return 0;
}

//向下調整建堆
int main()
{int a[] = {15,1,19,25,8,34,65,4,27,7 };

	//建堆---向下調整建堆---O(N)
	//向下調整建堆要從倒數的第一個非葉子節點開始向下調整，一直調整到根節點位置
	int n = sizeof(a) / sizeof(a[0]);
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{AdjustDown(a, n, i);
	}

	for (int i = 0; i< n; ++i)
	{printf("%d ", a[i]);
	}
	printf("\n");

	return 0;
}


//堆排序函數
//大思路：選擇排序，依次選數，從后往前排
//升序---先建大堆，建堆完畢后，此時大的數在第一位，把第一個和最后一個的位置進行交換，
// 交換完畢后，把最后一個不看做堆里面的，進行向下調整，選出次大的。后續依次類似處理。

//降序---先建小堆，建堆完畢后，此時最小的數在第一位，把第一個和最后一個的位置進行交換，
//交換完畢后，把最后一個不看做堆里面的，進行向下調整，選出次小的。后續依次類似處理。
void HeapSort(int* a, int n)
{//建堆---向下調整建堆---O(N)
	//向下調整建堆要從倒數的第一個非葉子節點開始向下調整，一直調整到根節點位置
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{AdjustDown(a, n, i);
	}

	//選數
	int i = 1;
	while (i< n)
	{Swap(&a[0], &a[n - i]);  //交換第一個數跟最后一個數
		AdjustDown(a, n - i, 0);
		++i;
	}
}
int main()
{int a[] = {15,1,19,25,8,34,65,4,27,7 };
	HeapSort(a, sizeof(a) / sizeof(int));

	for (size_t i = 0; i< sizeof(a) / sizeof(int); ++i)
	{printf("%d ", a[i]);
	}
	printf("\n");

	return 0;
}




//top k問題  N個數，找出這N個數中大的前k個數
int main()
{const char* filename = "Data.txt";
	int k = 3;
	PrintTopK(filename, k);

	return 0;
}

//在文件中隨機生成10000個數，然后找出其中前十個大數。
int main()
{const char* filename = "Data.txt";
	int N = 10000;
	int k = 10;

	CreateDataFile(filename, N);
	PrintTopK(filename, k);

	return 0;
}

你是否還在尋找穩定的海外服務器提供商？創新互聯www.cdcxhl.cn海外機房具備T級流量清洗系統配攻擊溯源，準確流量調度確保服務器高可用性，企業級服務器適合批量采購，新人活動首月15元起，快前往官網查看詳情吧

當前文章：【數據結構】建堆的方式、堆排序以及TopK問題-創新互聯
網頁地址：http://vcdvsql.cn/article36/djjcpg.html

成都網站建設公司_創新互聯，為您提供網站收錄、關鍵詞優化、網頁設計公司、用戶體驗、服務器托管、全網營銷推廣

廣告

聲明：本網站發布的內容（圖片、視頻和文字）以用戶投稿、用戶轉載內容為主，如果涉及侵權請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網站立場，如需處理請聯系客服。電話：028-86922220；郵箱：631063699@qq.com。內容未經允許不得轉載，或轉載時需注明來源： 創新互聯