? 理論部分

成都創新互聯成立以來不斷整合自身及行業資源、不斷突破觀念以使企業策略得到完善和成熟，建立了一套“以技術為基點，以客戶需求中心、市場為導向”的快速反應體系。對公司的主營項目，如中高端企業網站企劃 / 設計、行業 / 企業門戶設計推廣、行業門戶平臺運營、重慶APP開發公司、手機網站制作設計、微信網站制作、軟件開發、成都服務器托管等實行標準化操作，讓客戶可以直觀的預知到從成都創新互聯可以獲得的服務效果。

先補充一個概念，什么是路徑長度？

從樹中一個節點到另一個節點之間的分支構成這兩個節點之間的路徑，路徑上的分支數目稱作路徑長度。而一般不帶權的單個路徑長度默認為1，所以可以認為節點數為n的樹的路徑長度為n-1。

哈夫曼樹的定義是帶權路徑長度最短的樹，也叫最優二叉樹。換種更好的理解方式，就是一棵特殊的二叉樹，而這棵樹的葉子節點到根節點的帶權路徑都是盡可能最短的

如下圖：

樹a的路徑長度就是7*2+5*2+2*2+4*2=36。

樹b的路徑長度就是7*3+5*3+2*1+4*2=46

樹c的路徑長度就是7*1+5*2+2*3+4*3=35

明顯，樹c的路徑長度最小，但它是最優二叉樹嗎？

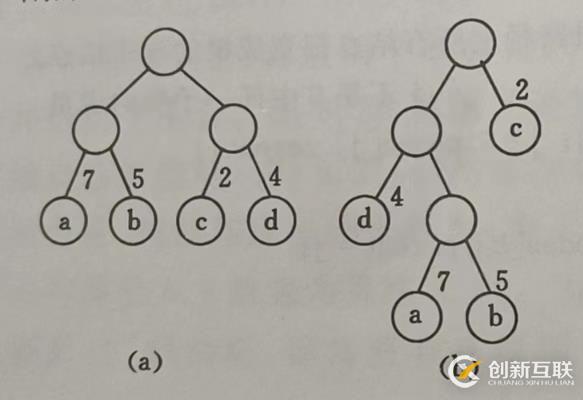想要驗證樹c是不是哈夫曼樹，就得從定義出發。帶權路徑長度最小，那么很容易想到，權重大的路徑所在的層數一定偏小，而權重小的路徑層數就偏小。那么很容易聯想到，把權重小的路徑先找出來并放在下面。經過總結可得出以下結論：

(1)根據給定的n個權值?{w1,w2,?,wn}?構成n棵二叉樹的集合?F={T1,T2,?,T?},?其中每棵二叉樹Ti中只有一個帶權為wi的根結點，其左右子樹均空。
(2)在F中選取兩棵根結點的權值最小的樹作為左右子樹構造一棵新的二叉樹，且置新的二叉樹的根結點的權值為其左、右子樹上根結點的權值之和。
(3)在F中刪除這兩棵樹，同時將新得到的二叉樹加入F中。
(4)重復(2)和(3)，直到F只含一棵樹為止。這棵樹便是赫夫曼樹。

哈夫曼編碼與前綴編碼：
前綴編碼:如果在一個編碼方案中， 任一個編碼都不是其他任何編碼的前綴(最左子串)，如稱編碼是前綴編碼。前綴編碼可以保證對壓縮文件進行解碼時不產生二義性，確保正確解碼。

哈夫曼編碼:對一棵具有n個葉子的哈夫曼樹，若對樹中的每個左分支賦予0，右分支賦予1,則從根到每個葉子的路徑上，各分支的賦值分別構成一一個二進制串，該二進制串就稱為哈夫曼編碼。
哈夫曼編碼是前綴編碼：哈夫曼編碼是根到葉子路徑上的編碼序列，由樹的特點知，若路徑A是另一條路徑B的最左部分，則B經過了A.則A的終點一定不是葉子，而哈夫曼編碼對應路徑的終點一定為葉子，因此，任一哈夫曼碼都不會與任意其他哈夫曼編碼的前綴部分完全重疊，因此哈夫曼編碼是前綴編碼。

哈夫曼編碼是最優前綴編碼：對于包括n個字符的數據文件，分別以它們的出現次數為權值構造哈夫曼樹，則利用該樹對應的哈夫曼編碼對文件進行編碼，能使該文件壓縮后對應的二進制文件的長度最短。

------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

實踐部分

以數據結構哈夫曼樹和哈夫曼編碼基礎題為例

請構建夫曼樹和哈夫曼編碼的實現，對于輸入的（n=8）個字符和對應的概率，生成其對應的哈夫曼編碼。

參考輸入如下：

"a","b","c","d","e","f","g","h"

0.07,0.19,0.02,0.06,0.32,0.03,0.21,0.1

參考輸出如下：

a:? ? ? ? 1010

b:? ? ? ? 00

c:? ? ? ? 10000

d:? ? ? ? 1001

e:? ? ? ? 11

f:? ? ? ? 10001

g:? ? ? ? 01

h:? ? ? ? 1011

首先是哈夫曼樹的定義，一般要求記錄節點的權重，雙親節點，左、右子女節點。

typedef struct{
    int weight;//權重
    int parents, Lchild, Rchlid;
}thnode,HuffmanTree[1000];

再是哈夫曼樹的構建，先對前n個（葉子）節點進行處理，記錄它們的權重，其他信息記為0。再對后面構建哈夫曼樹形成的過程節點（容易得知哈夫曼樹的節點個數為2*n-1個，所以過程節點有n-1個）的所有信息記為0。在根據理論部分的規律，進行哈夫曼樹的構建。

void Huffman_Creat(HuffmanTree ht,int w[],int n)//n為葉子結點個數
{
    //先處理前n個節點
    int m = 2 * n - 1;//樹的總結點數
    int i,s1,s2;
    for (i = 1; i<= n;i++)
    {
        ht[i].weight = w[i];
        ht[i].Lchild = 0;
        ht[i].Rchlid = 0;
        ht[i].parents = 0;
    }
    //再處理后面的過程節點
    for (i = n+1; i<= m;i++)
    {
        ht[i].weight = 0;
        ht[i].Lchild = 0;
        ht[i].Rchlid = 0;
        ht[i].parents = 0;
    }
    //最后再按規律構建哈夫曼樹
    for (i = n + 1; i<= m;i++)
    {
        select(ht, i - 1, &s1, &s2);//尋找雙親節點不為0的權重最小的2個節點
        ht[i].weight = ht[s1].weight + ht[s2].weight;
        ht[i].Lchild = s1;
        ht[i].Rchlid = s2;
        ht[s1].parents = i;
        ht[s2].parents = i;
    }
}

select函數就是尋找雙親節點不為0的權重最小的2個節點。

void select(HuffmanTree ht,int end,int*s1,int*s2)
{
    int min1, min2;//最小和第二小
    int i = 1;
    while(ht[i].parents!=0 && i<=end)
        i++;
    min1 = ht[i].weight;
    *s1 = i;

    i++;
    while(ht[i].parents!=0 && i<=end)
        i++;
    if(ht[i].weight=min1 && ht[j].weight

哈夫曼樹構建完成后，就是哈夫曼編碼的建立。利用定義中的parent，可以從葉子節點尋找回根節點，跟從根節點遍歷到葉子節點的方法相比，不但減少代碼量，還方便記錄過程編碼。

typedef char* HuffmanCode[1000];
void HuffmanCode_Creat(HuffmanTree ht, HuffmanCode hc,int n)
{
    char *s;
    int start;
    int i, c, p;
    s = (char *)malloc(n * sizeof(char));//創建臨時數組
    s[n - 1] = '\0';//反向存入s數組中，方便后續輸出
    for (i = 1; i<= n;i++)
    {
        start = n - 1;
        c = i;//存儲當前節點
        p = ht[i].parents;//存雙親
        while(p!=0)//只有根節點的雙親節點為0
        {
            --start;
            if(ht[p].Lchild==c)
                s[start] = '0';
            else
                s[start] = '1';
            c = p;
            p = ht[p].parents;//向上尋找雙親，直到為根節點
        }
        hc[i] = (char *)malloc((n - start) * sizeof(char));
        strcpy(hc[i], &s[start]);//將每次的結果存入hc數組
    }
    free(s);
}

結合本題要求，可得完整代碼為：

請代入個人思考，本代碼故意改了部分，輸出一定是錯誤的！！！

請代入個人思考，本代碼故意改了部分，輸出一定是錯誤的！！！

請代入個人思考，本代碼故意改了部分，輸出一定是錯誤的！！！

#includeusing namespace std;
typedef struct{
	char id;
    double weight;//權
    int parents, Lchild, Rchlid;
}thnode,HuffmanTree[1000];
void select(HuffmanTree ht,int end,int*s1,int*s2)
{
    double min1, min2;
    int i = 1;
    while(ht[i].parents!=0 && i<=end)
        i++;
    min1 = ht[i].weight;
    *s1 = i;

    i++;
    while(ht[i].parents!=0 && i<=end)
        i++;
    if(ht[i].weight=min1 && ht[j].weight>n;
    for (int i=1;i<=n;i++)
    	cin>>ppp[i];
    for (int i=1;i<=n;i++)
    	cin>>w[i];
    HuffmanTree ht;
    Huffman_Creat(ht, w, n);
	for (int i=1;i<=n;i++)
    	ht[i].id=ppp[i];
    HuffmanCode hc;
    HuffmanCode_Creat(ht,hc, n);
    for (i = 1; i<=n; i++)
      {
          printf("%c: %s\n", ht[i].id,hc[i]);
      }
    return 0;
}

你是否還在尋找穩定的海外服務器提供商？創新互聯www.cdcxhl.cn海外機房具備T級流量清洗系統配攻擊溯源，準確流量調度確保服務器高可用性，企業級服務器適合批量采購，新人活動首月15元起，快前往官網查看詳情吧

文章題目：C++哈夫曼樹和哈夫曼編碼詳解-創新互聯
本文來源：http://vcdvsql.cn/article36/ggspg.html

成都網站建設公司_創新互聯，為您提供搜索引擎優化、網站制作、靜態網站、定制網站、App設計、響應式網站

廣告

聲明：本網站發布的內容（圖片、視頻和文字）以用戶投稿、用戶轉載內容為主，如果涉及侵權請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網站立場，如需處理請聯系客服。電話：028-86922220；郵箱：631063699@qq.com。內容未經允許不得轉載，或轉載時需注明來源： 創新互聯