lc 606 根據(jù)二叉樹創(chuàng)建字符串

給你二叉樹的根節(jié)點 root ，請你采用前序遍歷的方式，將二叉樹轉(zhuǎn)化為一個由括號和整數(shù)組成的字符串，返回構(gòu)造出的字符串。

網(wǎng)站建設哪家好，找成都創(chuàng)新互聯(lián)公司！專注于網(wǎng)頁設計、網(wǎng)站建設、微信開發(fā)、小程序設計、集團企業(yè)網(wǎng)站建設等服務項目。為回饋新老客戶創(chuàng)新互聯(lián)還提供了博州免費建站歡迎大家使用！

空節(jié)點使用一對空括號對 “()” 表示，轉(zhuǎn)化后需要省略所有不影響字符串與原始二叉樹之間的一對一映射關系的空括號對。

題目描述：
從根開始，只要是兒子，就加一層（），**父節(jié)點和兒子之間一定要加()**如果2有單獨的孩子3,4，則是：2(3)(4)，而如果沒有左孩子而有右孩子，則：2()(4)。不加()不能區(qū)分是左孩子還是右孩子。
看圖：是一個dfs的感覺，只要有左孩子或右孩子，都該加()。因為就算只有右孩子，也要區(qū)分當前是右孩子。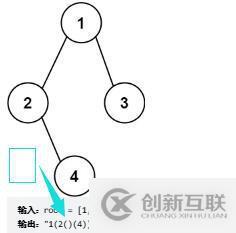

分析：
有兩種情況，我們都需要給左邊加：()。當左邊有值，需要加一圈()，當左邊無值而右邊有值，也需要多加()，不然只加不加()不能辨別是右邊的（）。
所以思路：

1. 若二叉樹不為空，則先根結(jié)點的值放入字符串。
2. 若左子樹不為空，或者左子樹為空但右子樹不為空，則需要將左子樹的值放入字符串。
3. 若右子樹不為空，則需要將右子樹的值放入字符串。

做法一：效率低，因為return字符串做拷貝構(gòu)造。

string tree2str(TreeNode* root) {string res = "";
        if (root == nullptr)
            return "";

        // 先把當前放入
        res += to_string(root->val);

        // 左不空 或 左為空但右不空 ：都需要放左邊的值或只給左邊加()。這兩個可以放一起
        if (root->left || root->right)
        {res += '(';
            res += tree2str(root->left);
            res += ')';
        }

        // 右不空 右子樹放字符串
        if (root->right)
        {res += '(';
            res += tree2str(root->right);
            res += ')';
        }
        return res;
    }

做法二：
將值放入?yún)?shù)上，就可以不用傳值而不斷讓它變長。注意過程中，別漏加每個節(jié)點上的本身值到字符串。

string tree2str(TreeNode* root) {if (root == nullptr)
            return "";
        string res = "";
        dfs(root, res);
        return res;
    }

    void dfs(TreeNode* root, string& res)
    {if (root == nullptr)
            return;
        // 把當前先加上
        res += to_string(root->val);
        // 左樹有或右樹有，都加
        if (root->left || root->right)
        {res += '(';
            dfs(root->left, res);
            res += ')';
        }
        // 右樹存在，就加上右樹值
        if (root->right)
        {res += '(';
            dfs(root->right, res);
            res += ')';
        }
    }

二叉樹的非遞歸遍歷

• 前序遍歷：
  前序遍歷的訪問順序是：根、左、右。
  做法：

1. 根節(jié)點和根的左孩子都是在左路節(jié)點上，如下圖所示，我們先挨著根、左孩子一直訪問， 這樣把左路節(jié)點都拿到了，再依次拿每個節(jié)點的右子樹上所有節(jié)點。比如：8、3、1，再拿1、3、8的右子樹上所有節(jié)點，這種順序符合棧結(jié)構(gòu)，所以具體做法看2。
   
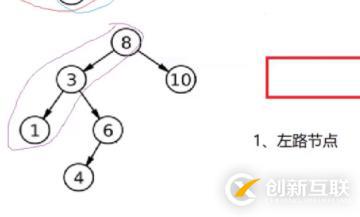
2. 具體做法：

1. 創(chuàng)建棧，初始化cur為根，依次拿根和根的左孩子入棧。
2. 依次出棧每個節(jié)點，如果節(jié)點存在右孩子，則更新cur為右孩子。
3. 整體需要一層循環(huán)（循環(huán)a），條件是：cur不為空或棧不為空。cur不為空，則循環(huán)（循環(huán)b while(cur)）著，去把當前和左孩子入棧。循環(huán)b如果做完了，說明局部子樹的左路節(jié)點都拿完了，我們需要彈棧首，更新cur，因為我們需要訪問每個節(jié)點的右子樹。
   cur = top->right;
4. 遍歷的值存入vector，我們可以開始就申請一個vector。關于存vector：在左路節(jié)點遍歷過程中，先序遍歷是優(yōu)先根原則，所以每次遇到一個根，就可以push。對于每個節(jié)點都會經(jīng)過內(nèi)存的循環(huán)，所以都會放到vector中去。
5. 記憶好該解題模板條件：while(cur || !st.empty())。

• 代碼

class Solution {public:
    vectorpreorderTraversal(TreeNode* root) {vectorv;
        stackst;
        TreeNode* cur = root;
        while(cur || !st.empty())
        {// 左路節(jié)點需要每次一股腦全加進來
            while(cur)
            {st.push(cur);
                v.push_back(cur->val);
                cur = cur->left;
            }
            // 當前走至最深的左節(jié)點的右路
            // 這里巧妙在每次右路節(jié)點，只能最深的一個右來更新cur
            TreeNode* top = st.top();
            st.pop();
            // cur可能不存在，但st可能還存在，就利用下次循環(huán)。
            cur = top->right;
        }
        return v;
    }
};

• 中序遍歷
  中序遍歷需要先左再根再右，比如下面的樹，8、3、1，在這個過程中，不能先按8、3、1去存，當沒有左孩子時，才可以考慮去存。所以和先序的區(qū)別在于，存vector得在第二層while()之后存值入vector。也就是說：

1. 每次到當前節(jié)點沒有左孩子，說明到達最左端，此時出棧頂，可以push該值。再轉(zhuǎn)cur至當前節(jié)點的右孩子。因為左和根是在一路的，push當前，其實也相當于push了根。
2. 中序其實是先序的微調(diào)整。
   

class Solution {public:
	vectorinorderTraversal(TreeNode* root) {stackst;
		vectorv;
		TreeNode* cur = root;
		while (cur || !st.empty())
		{	// 左路節(jié)點入棧
			while (cur)
			{		// 中序和前序的區(qū)別在出棧才能訪問
				st.push(cur);
				cur = cur->left;
			}
			// 當左路節(jié)點從棧中出來，表示左路節(jié)點已經(jīng)訪問過了，應該訪問根 這個節(jié)點和他的右子樹
			TreeNode* top = st.top();
			st.pop();
			v.push_back(top->val);
			cur = top->right;	// 子問題訪問右子樹
		}
		return v;
	}
};

• 后序遍歷
  
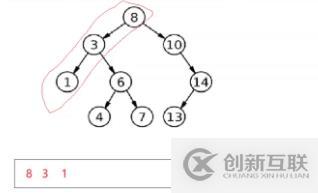
  如圖，后續(xù)遍歷的訪問順序是左、右、根，所以訪問一個節(jié)點時遵守的規(guī)則是：左右孩子均無，則訪問，如果有左孩子，則繼續(xù)深入。有右孩子，且訪問過，才能訪問當前。
  所以這里的做法是：前兩個的模板大體寫法不變，存一個prev記錄上一次訪問的節(jié)點。
  步驟：

1. 有左孩子則不斷深入更新cur，且放入棧st中，并更新prev。
2. 出循環(huán)更新cur，直到cur不存在，說明當前是局部最左孩子。
3. 然后出棧當前節(jié)點，當前節(jié)點如果有右孩子，則說明當前節(jié)點節(jié)點是個根，是根就不能訪問，不能存vector。但是還需要判斷，我們是第一次到達還是第二次到達這個根，所以判斷：top->right == nullptr或top->right == prev即：頂?shù)挠覟榭栈蝽數(shù)挠以L問過，則可以直接push當前值，并更新prev，如果這兩個條件不滿足，說明第一次來，或有右孩子，則更新cur到cur->right。
4. prev的更新只在push值之后，我們的真正訪問只有在push：val時，才算真正訪問。

class Solution {public:
	vectorpostorderTraversal(TreeNode* root) {stackst;
		vectorv;
		TreeNode* cur = root;
		TreeNode* prev = nullptr;
		while (cur || !st.empty())
		{	// 左路節(jié)點入棧
			while (cur)
			{		// 中序和前序的區(qū)別在出棧才能訪問
				st.push(cur);
				cur = cur->left;
			}
			// 當左路節(jié)點從棧中出來，表示左路節(jié)點已經(jīng)訪問過了，再訪問根這個節(jié)點的右子樹
			// 只要能下到這里來，就說明節(jié)點左孩子都訪問完了，可以訪問右孩子了
			TreeNode* top = st.top();
			// 當前節(jié)點沒有右子樹或訪問過了 可以入當前節(jié)點
			if (top->right == nullptr || top->right == prev)
			{		v.push_back(top->val);
				// 且可以出棧當前
				prev = top;	// 更新prev 說明這個節(jié)點訪問過了
				st.pop();
			}
			else
			{		cur = top->right;
			}
		}
		return v;
	}
};

JZ36. 二叉搜索樹與雙向鏈表

• 分析：二叉搜索樹變雙向鏈表，需要升序，所以以中序遍歷為模板，之前我們輸出節(jié)點放在inorder(root->left)和inorder(root->right)之間，而現(xiàn)在把輸出節(jié)點變?yōu)樽鲦溄印?/li>
• 思路：
  中序遞歸過程中，我們會最終先到最左節(jié)點，此時理論為頭節(jié)點，利用傳的參prev使得最左節(jié)點的left為prev，（prev初始為nullptr，正好使第一個節(jié)點前驅(qū)為nullptr）。在中間原本輸出的位置，判斷如果prev存在，則讓prev->right = cur（也就是root），不管prev存在不存在，prev都再需要變?yōu)閏ur。中序繼續(xù)往后走，遞歸去當前右子樹。

#includeusing namespace std;

struct TreeNode {int val;
	struct TreeNode* left;
	struct TreeNode* right;
	TreeNode(int x) :
		val(x), left(NULL), right(NULL) {}
}; 

class Solution {public:
    TreeNode* Convert(TreeNode* pRootOfTree) {TreeNode* prev = nullptr;
		inOrder(pRootOfTree, prev);
		TreeNode* head = pRootOfTree;
		while (head->left)
		{	head = head->left;
		}
		return head;
    }

	void inOrder(TreeNode* root, TreeNode* prev)
	{if (root == nullptr)
			return;
		inOrder(root->left, prev);	
		// op
		root->left = prev;
		if (prev)
		{	prev->right = root;
		}
		prev = root;
		inOrder(root->left, prev);
		
	}

};

最近公共祖先

普通二叉樹：leetcode236. 二叉樹的最近公共祖先

思路： 尋找從根到兩個節(jié)點的路徑，都放入棧中，棧頂是當前節(jié)點，棧底是根。找出兩個棧的高度差，棧深的先出棧差個節(jié)點，再依次比較兩個棧頂，第一個相等的節(jié)點就是最近祖先。

步驟：

1. find()求路徑函數(shù)：

1. 當前為空，返回false，說明走到了空節(jié)點位置還沒找到，就該返回，但是return false，因為發(fā)現(xiàn)找到時要返回true，停止去別的路徑遞歸。所以空節(jié)點位置是個出口。
2. 當前節(jié)點存在，就給棧：path中加入當前節(jié)點，如果當前值是所尋找，就返回true。
3. 否則繼續(xù)往左邊遞歸，但是加上判斷，如果在左邊遞歸能返回true，這里也返回true，不必往下遞歸去右。
4. 遞歸去右尋找。
5. 如果之前左右都找過，也沒能返回true而終止，說明當前節(jié)點不在路徑上。pop()當前節(jié)點，再返回false。 這里的false，返回后會返回到之前某一有孩子的節(jié)點上，繼續(xù)往別的方向走。

2. 求最近祖先：

1. 找兩個節(jié)點的路徑
2. 看哪個stack_size大，讓大的先出棧差個。
3. 挨個比較棧頂，不等就一直出棧。
4. 停下的時候必定相等， 此時哪個棧頂都正確。

bool findPath(TreeNode* root, TreeNode* x, stack& path)
    {if(root == nullptr)
            return false;
        path.push(root);    
        if(root->val == x->val)
            return true;
        // 左樹找到，就返回了，不去右樹
        if(findPath(root->left, x, path))
            return true;
        if(findPath(root->right, x, path))
            return true;
        path.pop(); // 節(jié)點左右子樹均沒有，該節(jié)不是路徑上節(jié)點
        return false;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {  stackppath, qpath;
              findPath(root, p, ppath);
              findPath(root, q, qpath);
              // 找到了路徑，然后都是倒著的，讓多的先刪掉差個
              
              stacklpath = ppath, spath=qpath;    // 區(qū)分長短路徑
              if(lpath.size()< spath.size())
              {  stackt = lpath;
                  lpath = spath;
                  spath = t;
              }
              int plus = lpath.size() - spath.size();
              while(plus--)
                lpath.pop();
              while(lpath.top()!=spath.top())
              {  lpath.pop();
                  spath.pop();
              }
           return lpath.top();
    }
};

• 搜索二叉樹：
  思路：
  尋找p、q，在BST樹中，最近祖先有兩種情況：（特殊情況）其中之一是根，則根是最近公共祖先，因為從上往下訪問。（普通情況）最近公共祖先一定是大于其中之一而小于另外一個。

特殊情況如下：遍歷按從上往下，先根再次根，比如m和n或p和q，都是一個根，而另外一個處于一個根的情況，如果我們訪問到當前節(jié)點是p、q中某一個，說明某個節(jié)點處于另外一個節(jié)點的局部根位置。

普通情況下，如0、3的最近祖先1或0、6的最近祖先5，也或者0、4的最近祖先1，都滿足大于其中一個、小于另外一個。

所以步驟如下：

1. 當前節(jié)點是p或q中某一個，則當前就是答案
2. 當前節(jié)點比兩個都小，cur去當前的左邊；當前節(jié)點比兩個都大，cur去當前的右邊。
3. 當前節(jié)點比一個大，比另一個小，就是最小公共祖先。

注意

1. 上面過程不會運行到某個不存在的節(jié)點，因為BST按上面的規(guī)則不會走到空。
2. 每組情況，都要返回，不管是全大還是全小，都得返回

• 代碼

class Solution {public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root->val == p->val || root->val == q->val)  // 如果某個節(jié)點是其中之一，其實比本身值也可以
        {return root;
        }
        // 不會當前不存在的節(jié)點上
        if(root->val< p->val && root->val< q->val)
            return lowestCommonAncestor(root->right, p, q);
        else if(root->val >p->val && root->val >q->val)
            return lowestCommonAncestor(root->left, p, q);
        else
            return root;
    }
};

重建二叉樹

• 思路：
  用一個函數(shù)即可，當前函數(shù)就行。
  去創(chuàng)建樹，參數(shù)是2個vector順序，然后兩個數(shù)組的4個邊界。
  在前序中，確定根值，再去中序找根位置，每次創(chuàng)建當前節(jié)點，然后再遞歸鏈去左和右，遞歸鏈接左右。

class Solution {public:
	TreeNode* createMyTree(vector& pre, int pleft, int pright, vector& in, int inleft, int inright)
	{//cout<< "pleft = "<< pleft<< " , pright = "<< pright<< " , inleft = "<< inleft<< " , inright = "<< inright<< endl;
		// 出口一定要記好：等于的話，也需要建一個節(jié)點 大于才停止
		if (pleft>pright )
		{	return nullptr;
		}
		
		// 每次根節(jié)點和根節(jié)點的左右邊界
		TreeNode* root = new TreeNode(pre[pleft]);
		// 前序中的第一個是根，根在中序中位置
		int root_Inorder_Index = 0;
		for (int i = inleft; i<= inright; i++)
		{	if (pre[pleft] == in[i])
			{		root_Inorder_Index = i;
				break;
			}
		}
		// 因為前面就錯了，沒找到。
		// cout<< "當前前序根："<< pre[pleft]<< " , 中序中是："<< in[root_Inorder_Index]<< " , 位置："<< root_Inorder_Index<< endl;
		// 左子樹個數(shù)：
		int Lnums = root_Inorder_Index-inleft;
		// 右子樹個數(shù)：
		//int Rnums = inright - root_Inorder_Index;
		//cout<< "左子樹："<< Lnums<< ", 右子樹："<< Rnums<< endl;
		// 利用左右子樹的數(shù)量，分別拿節(jié)點
		root->left = createMyTree(pre, pleft+1, pleft+Lnums, in, inleft, root_Inorder_Index-1);
		root->right = createMyTree(pre, pleft+Lnums+1, pright, in, root_Inorder_Index+1, inright);
		return root;
	}
	// 遞歸建樹	另用遞歸函數(shù)
	TreeNode* buildTree(vector& preorder, vector& inorder) {if (preorder.size() == 0)
			return nullptr;
		TreeNode* root = createMyTree(preorder, 0, preorder.size()-1, inorder, 0, inorder.size()-1);
		return root;
	}
};

中序和后續(xù)遍歷構(gòu)造二叉樹

leetcode 106. 從中序與后序遍歷序列構(gòu)造二叉樹

class Solution {public:
	TreeNode* create(vector& in, int s1, int e1, vector& post, int s2, int e2)
	{if (s1 >e1 || s2 >e2)
			return nullptr;
		TreeNode* root = new TreeNode(post[e2]);
		int rootOfIn = 0;
		for (int i = s1; i<= e1; i++)
		{	if (post[e2] == in[i])
			{		rootOfIn = i;
				break;
			}
		}
		int Lnums = rootOfIn-s1;
		root->left = create(in, s1, rootOfIn-1, post, s2, s2+Lnums-1);
		root->right = create(in, rootOfIn+1, e1, post, s2+Lnums, e2-1);
		return root;
	}


	TreeNode* buildTree(vector& inorder, vector& postorder) {if (inorder.size() == 0)
			return nullptr;
		TreeNode* root = create(inorder, 0, inorder.size()-1, postorder, 0, postorder.size()-1);
		return root;
	}
};

二叉搜索樹與雙向鏈表

錯的

class Solution {public:
	void Inorder(TreeNode* root, TreeNode* prev)
	{// 訪問到空 就返回
		if(root == nullptr)
			return;
		Inorder(root->left, prev);
		// 原本輸出值的地方，我們給它換成做鏈接：一左一右
		root->left = prev;
		if(prev)	// 除了中序第一個節(jié)點時，prev是null，其它prev都有值
		{	prev->right = root;
		}
		// 只有當前節(jié)點的左，全訪問完，才能輪到當前做prev，且它是以它為根，右孩子的prev。
		prev = root;
		Inorder(root->right, prev);
	}
    TreeNode* Convert(TreeNode* pRootOfTree) {if(pRootOfTree == nullptr)
			return nullptr;
		// 按中序遍歷走
		TreeNode* prev = nullptr;
		TreeNode* head = pRootOfTree;
		Inorder(head, prev);
		while(head)
		{	head = head->left;
		}
		return head; 
	}
};

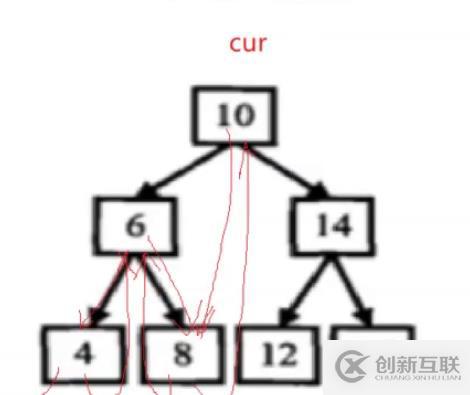
以上錯了，錯在prev在不斷改變，比如cur在14的那個節(jié)點，而prev上一次是10，cur可以通過cur->left遞歸到12，也可以通過cur->right遞歸到16，但是對于cur為14，給12、16傳入的prev是10，我們需要prev每次都做出改變，所以prev用指針的引用，但cur每次會自動隨著遞歸函數(shù)的傳值而變化。

你是否還在尋找穩(wěn)定的海外服務器提供商？創(chuàng)新互聯(lián)www.cdcxhl.cn海外機房具備T級流量清洗系統(tǒng)配攻擊溯源，準確流量調(diào)度確保服務器高可用性，企業(yè)級服務器適合批量采購，新人活動首月15元起，快前往官網(wǎng)查看詳情吧

名稱欄目：C++：二叉樹題進階（三種非遞歸遍歷、二叉搜索樹OJ題）-創(chuàng)新互聯(lián)
網(wǎng)站鏈接：http://vcdvsql.cn/article4/diopoe.html

成都網(wǎng)站建設公司_創(chuàng)新互聯(lián)，為您提供軟件開發(fā)、建站公司、ChatGPT、網(wǎng)站設計、微信小程序、電子商務

廣告

聲明：本網(wǎng)站發(fā)布的內(nèi)容（圖片、視頻和文字）以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主，如果涉及侵權請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網(wǎng)站立場，如需處理請聯(lián)系客服。電話：028-86922220；郵箱：631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載，或轉(zhuǎn)載時需注明來源： 創(chuàng)新互聯(lián)