這篇文章主要講解了“javascript如何求素數”，文中的講解內容簡單清晰，易于學習與理解，下面請大家跟著小編的思路慢慢深入，一起來研究和學習“javascript如何求素數”吧！

10多年的青浦網站建設經驗，針對設計、前端、開發、售后、文案、推廣等六對一服務，響應快，48小時及時工作處理。營銷型網站建設的優勢是能夠根據用戶設備顯示端的尺寸不同，自動調整青浦建站的顯示方式，使網站能夠適用不同顯示終端，在瀏覽器中調整網站的寬度，無論在任何一種瀏覽器上瀏覽網站，都能展現優雅布局與設計，從而大程度地提升瀏覽體驗。創新互聯從事“青浦網站設計”,“青浦網站推廣”以來，每個客戶項目都認真落實執行。

求素數的方法：1、遍歷1~n區間中的所有自然數給n來除，若余數為0則表示該數n不是素數，否則就是素數，語法“for(i=2;i<n;i++){if(n%i===0){return false;}}”。2、利用素數平方根范圍，語法“for(i=2;i<=Math.sqrt(n);i++){if(n%i===0){return false;}}”。

本教程操作環境：windows7系統、javascript1.8.5版、Dell G3電腦。

素數的概念

素數又叫質數，素數是指在大于1的自然數中，除了1和它本身以外，不能被其他自然數整除的數。

100以內的素數：2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97，共計25個。

JavaScript判定素數的四種方法

1、素數只能被1和自身整除

素數只能被1和自身整除，所以遍歷（1，n）開區間中的所有自然數給n來除，若存在整除，即余數為0，則表示該數n不是素數，否則就是素數。

function isPrime(n) {
  n = parseInt(n);
 
  if (n <= 3) {
    return n > 1;
  }
 
  for (let i = 2; i < n; i++) {
    if (n % i === 0) {
      return false;
    }
  }
  return true;
}

但是這種算法的復雜度為O(n)

2、素數平方根范圍

假設n不是素數，則n除了可以被1和n整除外，還可以被i、j整除，即 n / i = j...0，比如15不是素數，15 / 3 = 5，比如35不是素數，35 / 5 = 7，此時i,j必然分別處于(1, Math.sqrt(n)]和[Math.sqrt(n), n） 之中，比如Math.sqrt(15) ≈ 3.8，則 3處于（1，3.8]，5處于[3.8, 15）。比如Math.sqrt(4) = 2，則2處于(1,2]中，也處于[2,4)中。

function isPrime(n) {
  n = parseInt(n);
 
  if (n <= 3) {
    return n > 1;
  }
 
  for (let i = 2; i <= Math.sqrt(n); i++) {
    if (n % i === 0) {
      return false;
    }
  }
  return true;
}

此時算法復雜度為O（sqrt(n)）

3、素數不能非2的其他偶數

除了2，所有偶數都不是素數

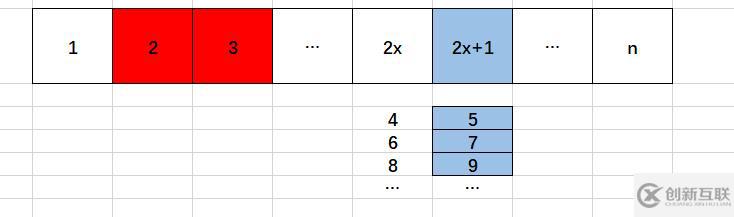
function isPrime(n) {
  n = parseInt(n);
 
  if (n <= 3) {
    return n > 1;
  }
 
  if (n % 2 === 0) {
    return false;
  }
 
  for (let i = 3; i <= Math.sqrt(n); i += 2) {
    if (n % i === 0) {
      return false;
    }
  }
  return true;
}

for循環中n，只能為上圖淺藍色部分。

因此上面算法減少了一半的循環，時間復雜度為O（sqrt(n) / 2）

需要注意的是，本算法的代碼不能將n % 2 === 0 的判斷條件加入到循環中，如下代碼存在漏洞

function isPrime(n) {
  n = parseInt(n);
 
  if (n <= 3) {
    return n > 1;
  }
 
  for (let i = 3; i <= Math.sqrt(n); i += 2) {
    if (n % 2 === 0 || n % i === 0) {
      return false;
    }
  }
  return true;
}

此時4、6、8都會被判定為素數。

漏洞形成的原因是，for循環的循環條件 i <= Math.sqrt(n) 不成立，比如n=4時，i <= Math.sqrt(4) 不成立，導致n無法進入循環中n % 2 === 0 的判斷，而是直接退出循環，return true。

該算法只能保證循環條件   i <= Math.sqrt(n) 成立的n值判斷素數正確，即 n >= i^2 = 9 時。

4、大于等于5的素數一定和6的倍數相鄰

大于等于5的素數一定和6的倍數相鄰

（注意這句話不等價于：和6的倍數相鄰的數一定是大于5的素數，該結論不成立。）

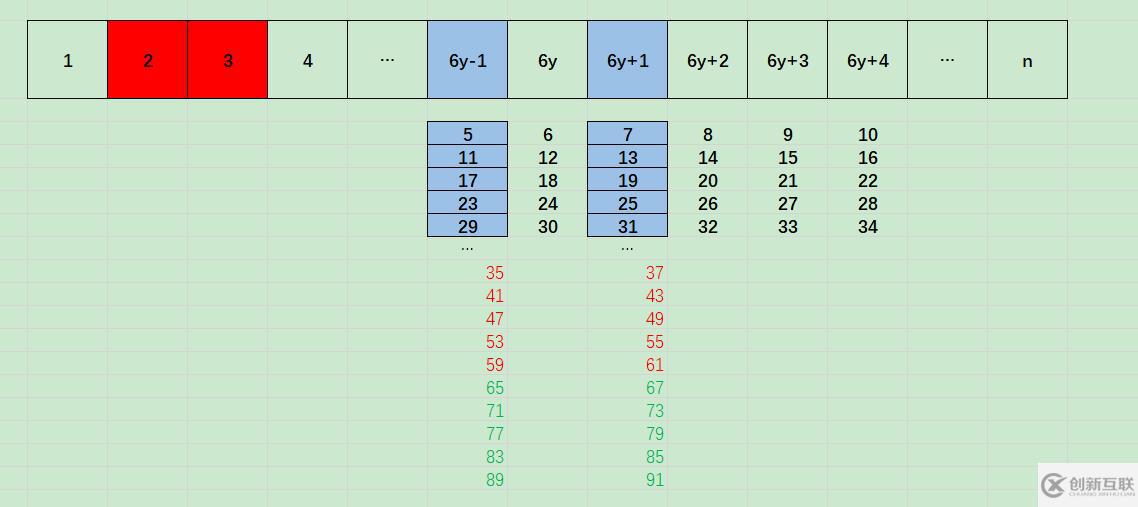
如上圖中，將大于等于5的數分為了：6y-1、6y、6y+1、6y+2、6y+3、6y+4（y>=1）

其中，6y、6y+2、6y+3、6y+4都不可能是素數，只有6y-1和6y+1可能是素數。

另外，6y-1（y>=1）和 6y + 5 （y>=0）等價。

所以，我們可以將n不為6y-1（或6y+5）和6y+1的數直接排除，排除方法為，

  if (n % 6 !== 1 && n % 6 !== 5) {
    return false;
  }

下面要剔除掉6y-1（或6y+5）和6y+1中的非素數，

  for (let i = 5; i <= Math.sqrt(n); i += 6) {
    if (n % i === 0 || n % (i + 2) === 0) {
      return false;
    }
  }

這里大家比較疑惑的可能有兩點：

• for循環i自增為啥是 6

• for循環中素數判定的條件為啥是 n % i === 0 || n % (i+2) === 0

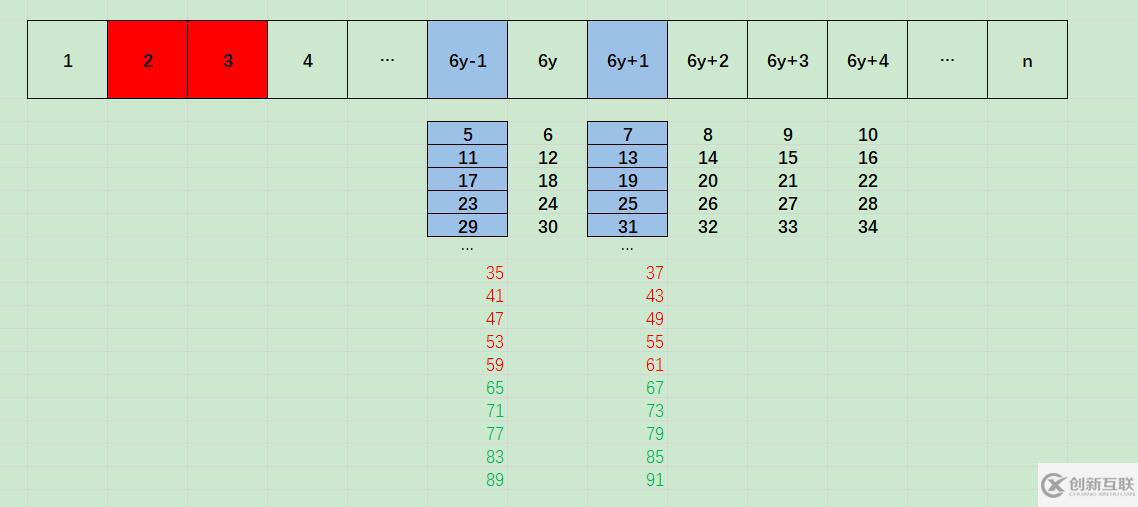
我們看上面圖解，可以發現，6y-1，是基數為5，差值為6的等差數列，即 5 + 6x :

• 對于 5 + 6x 而言，如果x為5的倍數（5 * z），則5 + 6x = 5 + 6 * 5 * z = 5 *（1+6z）,則此時5 + 6x可以被5整除。

• 5 + 6x 還可以轉化為 5 + 6 + 6 * (x-1) = 11 + 6(x-1)，則只要x-1為11的倍數，則5 + 6x可以被11整除，

• 5 + 6x 還可以轉化為 5 + 12 + 6 * (x-2) = 17 + 6(x-2)，則只要x-2為17的倍數，則5 + 6x可以被17整除

• ......

6y+1，是基數為7，差值為6的等差數列，即 7 + 6x :

• 對于 7 + 6x 而言，如果x為7的倍數（7 * z），則7 + 6x = 7 + 6 * 7 * z = 7 *（1+6z）,則此時7 + 6x可以被7整除。

• 7 + 6x 還可以轉化為 7 + 6 + 6 * (x-1) = 13 + 6(x-1)，則只要x-1為13的倍數，則7 + 6x可以被13整除，

• 7 + 6x 還可以轉化為 7 + 12 + 6 * (x-2) = 19 + 6(x-2)，則只要x-2為19的倍數，則7 + 6x可以被19整除，

• ......

所以6y-1和6y+1可能整除的數自增量為6，這是for循環i自增為啥是 6的原因

且6y-1和6y+1的整除數基數為5和7，相差為2，這是for循環中素數判定的條件為啥是 n % i === 0 || n % (i+2) === 0的原因

function isPrime(n) {
  n = parseInt(n);
 
  if (n <= 3) {
    return n > 1;
  }
 
  if (n % 6 !== 1 && n % 6 !== 5) {
    return false;
  }
 
  for (let i = 5; i <= Math.sqrt(n); i += 6) {
    if (n % i === 0 || n % (i + 2) === 0) {
      return false;
    }
  }
 
  return true;
}

此時時間復雜度為 O（sqrt(n) / 3）

感謝各位的閱讀，以上就是“javascript如何求素數”的內容了，經過本文的學習后，相信大家對javascript如何求素數這一問題有了更深刻的體會，具體使用情況還需要大家實踐驗證。這里是創新互聯，小編將為大家推送更多相關知識點的文章，歡迎關注！

網站標題：javascript如何求素數
網站URL：http://vcdvsql.cn/article4/gjigie.html

成都網站建設公司_創新互聯，為您提供品牌網站制作、外貿建站、網站設計公司、微信小程序、網站制作、定制網站

廣告

聲明：本網站發布的內容（圖片、視頻和文字）以用戶投稿、用戶轉載內容為主，如果涉及侵權請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網站立場，如需處理請聯系客服。電話：028-86922220；郵箱：631063699@qq.com。內容未經允許不得轉載，或轉載時需注明來源： 創新互聯