數據結構（十三）——樹

一、樹的簡介

1、樹的簡介

樹是一種非線性的數據結構，是由n（n >=0）個結點組成的有限集合。
如果n==0，樹為空樹。
如果n>0，
樹有一個特定的結點，根結點
根結點只有直接后繼，沒有直接前驅。
除根結點以外的其他結點劃分為m（m>=0）個互不相交的有限集合，T0，T1，T2，...，Tm-1，每個結合是一棵樹，稱為根結點的子樹。
樹的示例如下：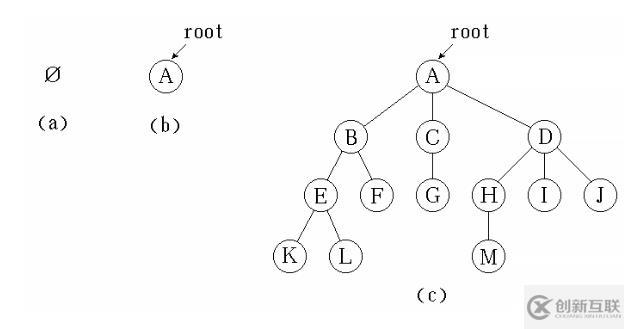

成都創新互聯專業為企業提供達茂旗網站建設、達茂旗做網站、達茂旗網站設計、達茂旗網站制作等企業網站建設、網頁設計與制作、達茂旗企業網站模板建站服務，10多年達茂旗做網站經驗，不只是建網站，更提供有價值的思路和整體網絡服務。

2、樹的度

樹的結點包含一個數據和多個指向子樹的分支
結點擁有的子樹的數量為結點的度，度為0的結點是葉結點，度不為0的結點為分支結點，樹的度定義為樹的所有結點中度的最大值。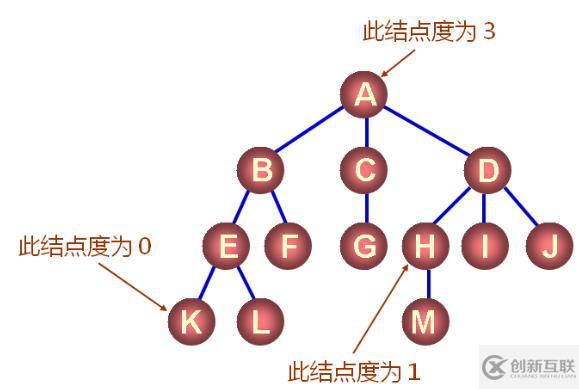

3、樹的前驅和后繼

結點的直接后繼稱為結點的孩子，結點稱為孩子的雙親。
結點的孩子的孩子稱為結點的孫子，結點稱為子孫的祖先。
同一個雙親的孩子之間互稱兄弟。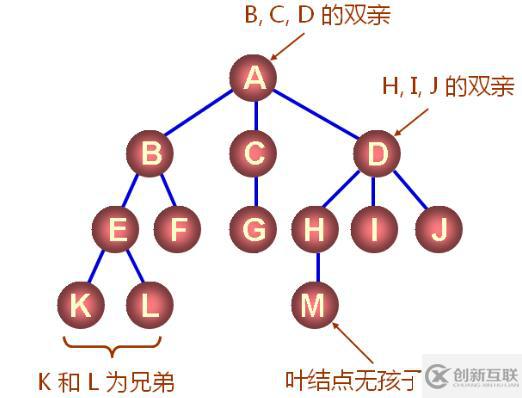

4、樹中結點的層次

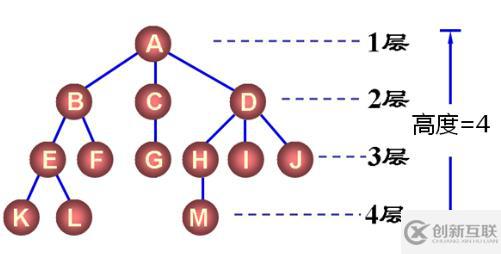
樹中根結點為第1層，根結點的孩子為第2層，依次類推。
樹中結點的最大層次稱為樹的深度或高度

5、樹的有序性

如果樹中結點的各子樹從左向右是有序的，子樹間不能互換位置，則稱該樹為有序樹，否則為無序樹。

6、森林

森林是由n棵互不相交的樹組成的集合。
三棵樹組成的森林如下：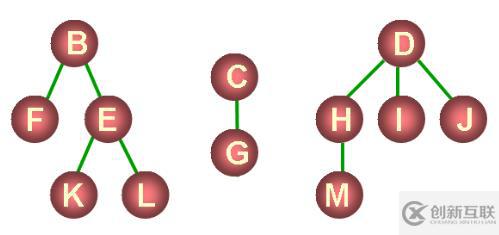

二、樹的抽象實現

1、樹的抽象實現

樹在程序中表現為一種特殊的數據類型。
樹的抽象實現如下：

template <typename T>
  class Tree:public Object
  {
  protected:
    TreeNode<T>* m_root;//根結點
  public:
    Tree(){m_root = NULL;}
    //插入結點
    virtual bool insert(TreeNode<T>* node) = 0;
    virtual bool insert(const T& value, TreeNode<T>* parent) = 0;
    //刪除結點
    virtual SharedPointer< Tree<T> > remove(const T& value) = 0;
    virtual SharedPointer< Tree<T> > remove(TreeNode<T>* node) = 0;
    //查找結點
    virtual TreeNode<T>* find(const T& value)const = 0;
    virtual TreeNode<T>* find(TreeNode<T>* node)const = 0;
    //根結點訪問函數
    virtual TreeNode<T>* root()const = 0;
    //樹的度訪問函數
    virtual int degree()const = 0;
    //樹的高度訪問函數
    virtual int height()const = 0;
    //樹的結點數目訪問函數
    virtual int count()const = 0;
    //清空樹
    virtual void clear() = 0;
  };

2、樹結點的抽象實現

樹中的結點表現為一種特殊的數據類型。
結點的抽象實現如下：

template <typename T>
  class TreeNode:public Object
  {
  public:
    T value;
    TreeNode<T>* parent;
    TreeNode()
    {
      parent = NULL;
    }
    virtual ~TreeNode() = 0;
  };
  template <typename T>
  TreeNode<T>::~TreeNode()
  {
  }

三、樹的操作

1、樹和樹結點的存儲結構實現

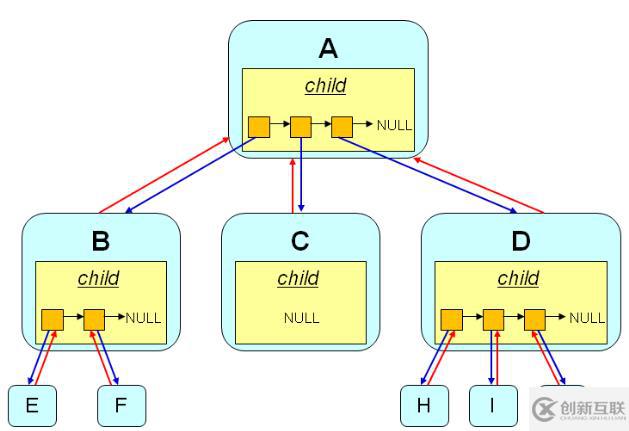
GTreeNode能夠包含任意多個指向后繼結點的指針。

template <typename T>
  class GTreeNode:public TreeNode<T>
  {
  protected:
    LinkedList<GTreeNode<T>*> m_children;
  };
GTree為通用樹結構，每個結點可以存在多個后繼結點。
  template <typename T>
  class GTree:public Tree<T>
  {
  public:
  };

每個樹結點包含指向前驅結點的指針，優點在于可以將非線性的樹轉化為線性的結構。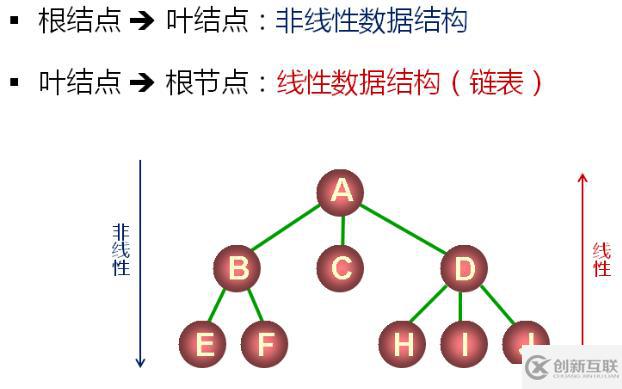

2、樹中結點的查找

A、基于數據元素值的查找
定義在任意一個結點為根結點的樹中查找指定數據元素值所在的結點的函數。

GTreeNode<T>* find(GTreeNode<T>* node, const T& value)const
    {
      GTreeNode<T>* ret = NULL;
      if(node != NULL)
      {
          //如果根結點的就是目標結點
          if(node->value == value)
          {
              ret =  node;
          }
          else
          {
              //遍歷根節點的子結點
              for(node->m_children.move(0); !node->m_children.end() && (ret == NULL); node->m_children.next())
              {
                  //對每個子子結點進行查找
                  ret = find(node->m_children.current(), value);
              }
          }
      }
      return ret;
    }

    //查找結點
    virtual GTreeNode<T>* find(const T& value)const
    {
      return find(root(), value);
    }

B、基于樹中結點的查找
定義在任意一個結點為根結點的樹中查找指定結點的函數

 GTreeNode<T>* find(GTreeNode<T>* node, GTreeNode<T>* obj)const
    {
      GTreeNode<T>* ret = NULL;
      //根結點為目標結點
      if(node == obj)
      {
          ret =  node;
      }
      else
      {
          if(node != NULL)
          {
              //遍歷子結點
              for(node->m_children.move(0); !node->m_children.end() && (ret == NULL); node->m_children.next())
              {
                  ret = find(node->m_children.current(), obj);
              }
          }
      }
      return ret;
    }

    virtual GTreeNode<T>* find(TreeNode<T>* node)const
    {
      return find(root(), dynamic_cast<GTreeNode<T>*>(node));
    }

3、樹中結點的插入

樹是非線性的數據結構，無法采用下標的方式定位數據元素，由于每個結點的都有一個唯一的前驅結點（父結點），因此必須找到前驅結點才能找到插入的位置。
A、插入結點
插入結點的流程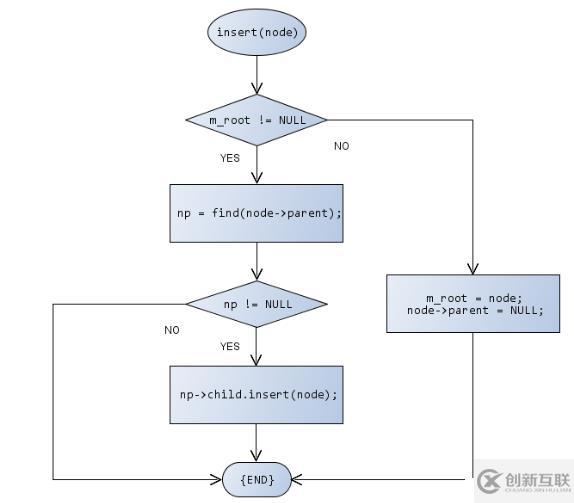

bool insert(TreeNode<T>* node)
    {
      bool ret = true;
      if(node != NULL)
      {
          //樹為空，插入結點為根結點
          if(this->m_root == NULL)
          {
              node->parent = NULL;
              this->m_root = node;
          }
          else
          {
              //找到插入結點的父結點
              GTreeNode<T>* np = find(node->parent);
              if(np != NULL)
              {
                  GTreeNode<T>* n = dynamic_cast<GTreeNode<T>*>(node);
                  //如果子結點中無該結點，插入結點
                  if(np->m_children.find(n) < 0)
                  {
                      ret = np->m_children.insert(n);
                  }
              }
              else
              {
                  THROW_EXCEPTION(InvalidOperationException, "Invalid node...");
              }
          }
      }
      else
      {
          THROW_EXCEPTION(InvalidParameterException, "Parameter is invalid...");
      }
      return ret;
    }

B、插入數據元素
插入數據元素到樹中的流程如下：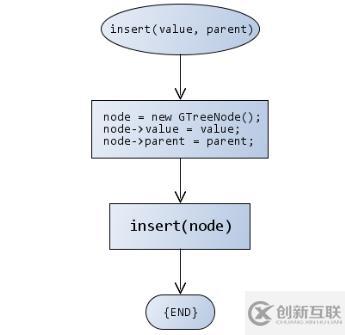

bool insert(const T& value, TreeNode<T>* parent)
    {
      bool ret = true;
      GTreeNode<T>* node = GTreeNode<T>::NewNode();
      if(node != NULL)
      {
          node->value = value;
          node->parent = parent;
          insert(node);
      }
      else
      {
          THROW_EXCEPTION(NoEnoughMemoryException, "No enough memory...");
      }
      return ret;
    }

4、樹中結點的清除

樹的清空操作需要將樹中所有的結點清除，并釋放分配在堆中的結點。
定義清除樹中每個結點的函數

如果樹中的結點可能分配在棧上和堆上，需要將堆空間的結點進行釋放。
根據內存地址不能準確判斷結點所在的存儲空間，清除時存儲在棧上的結點并不需要釋放，只需要釋放存儲在堆空間的結點。
使用工廠模式對分配在堆空間的結點進行定制。
A、GTreeNode類中增加保護的堆空間標識成員m_flag
B、重載GTreeNode的operrator new操作符，聲明為保護
C、提供工廠方法NewNode（），在工廠方法中創建堆空間的結點，并將m_flag標識置為true。

template <typename T>
  class GTreeNode:public TreeNode<T>
  {
  protected:
    bool m_flag;//堆空間標識
    //重載new操作符，聲明為保護
    void* operator new(unsigned int size)throw()
    {
      return Object::operator new(size);
    }

  public:
    LinkedList<GTreeNode<T>*> m_children;
    GTreeNode()
    {
      //棧上分配的空間標識為false
      m_flag = false;
    }
    //工廠方法，創建堆空間的結點
    static GTreeNode<T>* NewNode()
    {
      GTreeNode<T>* ret = new GTreeNode<T>();
      if(ret != NULL)
      {
          //堆空間的結點標識為true
          ret->m_flag = true;
      }
      return ret;
    }
    //堆空間結點標識訪問函數
    bool flag()const
    {
      return m_flag;
    }
  };
結點的釋放：
    void free(GTreeNode<T>* node)
    {
      if(node != NULL)
      {
          for(node->m_children.move(0); !node->m_children.end(); node->m_children.next())
          {
              free(node->m_children.current());
          }
          //如果結點存儲在堆空間
          if(node->flag())
             delete node;//釋放
      }
    }
清空樹：
    void clear()
    {
        free(root());
        this->m_root = NULL;
    }

5、樹中結點的刪除

刪除函數的設計要點：
將被刪除結點的子樹進行刪除；
刪除函數返回一顆堆空間的樹；
具體返回值為指向樹的智能指針；
具體的結點刪除功能函數如下：
將node為根結點的子樹從原來的樹中刪除，ret作為子樹返回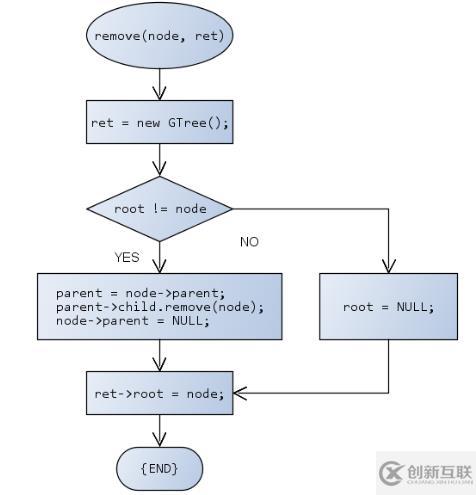

void remove(GTreeNode<T>* node, GTree<T>*& ret)
    {
      ret = new GTree<T>();
      if(ret != NULL)
      {
          //如果刪除的結點是根結點
          if(root() == node)
          {
              this->m_root = NULL;
          }
          else
          {
              //獲取刪除結點的父結點的子結點鏈表
              LinkedList<GTreeNode<T>*>& child = dynamic_cast<GTreeNode<T>*>(node->parent)->m_children;
              //從鏈表中刪除結點
              child.remove(child.find(node));
              //結點的父結點置NULL
              node->parent = NULL;
          }
          //將刪除結點賦值給創建的樹ret的根結點
          ret->m_root = node;
      }
      else
      {
          THROW_EXCEPTION(NoEnoughMemoryException, "No enough memory...");
      }
    }

A、基于刪除數據元素值刪除結點

 SharedPointer<Tree<T>> remove(const T& value)
    {
      GTree<T>* ret = NULL;
      //找到結點
      GTreeNode<T>* node = find(value);
      if(node != NULL)
      {
          remove(node, ret);
      }
      else
      {
          THROW_EXCEPTION(InvalidParameterException, "Parameter invalid...");
      }
      return ret;
    }

B、基于結點刪除

 SharedPointer<Tree<T>> remove(TreeNode<T>* node)
    {
      GTree<T>* ret = NULL;
      node = find(node);
      if(node != NULL)
      {
          remove(dynamic_cast<GTreeNode<T>*>(node), ret);
      }
      else
      {
          THROW_EXCEPTION(InvalidParameterException, "Parameter invalid...");
      }
      return ret;
    }

6、樹中結點的屬性操作

A、樹中結點的數量
以node為結點的子樹的結點數量，遞歸模型如下：

int count(GTreeNode<T>* node) const
    {
      int ret = 0;
      if(node != NULL)
      {
          ret = 1;//根結點
          //遍歷根節點的子結點
          for(node->m_children.move(0); !node->m_children.end(); node->m_children.next())
          {
              ret += count(node->m_children.current());
          }
      }
      return ret;
    }
    //樹的結點數目訪問函數
    int count()const
    {
        count(root());
    }

B、樹的度
結點node為根的樹的度的功能函數的遞歸模型如下：

int degree(GTreeNode<T>* node) const
    {
      int ret = 0;
      if(node != NULL)
      {
          //結點的子結點的數量
          ret = node->m_children.length();
          //遍歷子結點
          for(node->m_children.move(0); !node->m_children.end(); node->m_children.next())
          {
              int d = degree(node->m_children.current());
              if(ret < d)
              {
                  ret = d;
              }
          }
      }
      return ret;
    }

    //樹的度訪問函數
    int degree()const
    {
        return degree(root());
    }

C、樹的高度
結點node為根的樹的高度的功能函數的遞歸模型如下：

int height(GTreeNode<T>* node)const
    {
      int ret = 0;
      if(node != NULL)
      {
          //遍歷子結點
          for(node->m_children.move(0); !node->m_children.end(); node->m_children.next())
          {
              //當前結點的高度
              int h = height(node->m_children.current());
              if(ret < h)
              {
                  ret = h;
              }
          }
          ret = ret + 1;
      }
      return ret;
    }
    //樹的高度訪問函數
    int height()const
    {
        height(root());
    }

7、樹中結點的遍歷

樹是一種非線性的數據結構，遍歷樹中結點可以采用游標的方式。
A、在樹中定義一個游標（GTreeNode<T>* node）
B、遍歷開始前將游標指向根結點
C、獲取游標指向的數據元素
D、通過結點中的m_children成員移動游標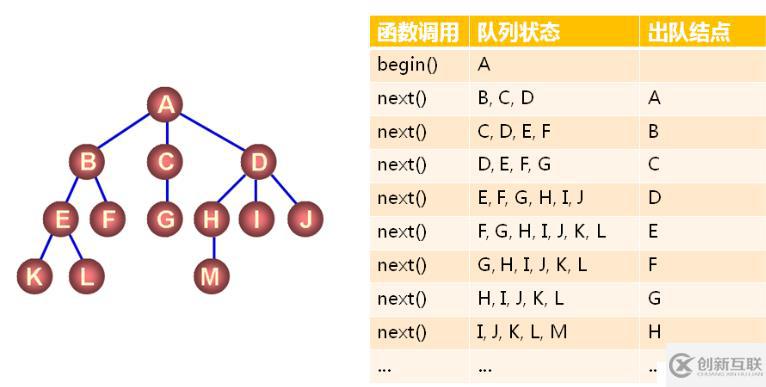

將根結點壓入隊列中

 bool begin()
    {
      bool ret = (root() != NULL);
      if(ret)
      {
          //清空隊列
          m_queue.clear();
          //根節點加入隊列
          m_queue.add(root());
      }
      return ret;
    }

判斷隊列是否為空

 bool end()
    {
        return (m_queue.length() == 0);
    }

隊頭元素彈出，將隊頭元素的孩子壓入隊列中

 bool next()
    {
      bool ret = (m_queue.length() > 0);
      if(ret)
      {
          GTreeNode<T>* node = m_queue.front();
          m_queue.remove();//隊頭元素出隊
          //將隊頭元素的子結點入隊
          for(node->m_children.move(0); !node->m_children.end(); node->m_children.next())
          {
              m_queue.add(node->m_children.current());
          }
      }
      return ret;
    }

訪問隊頭元素指向的數據元素

T current()
    {
      if(!end())
      {
          return m_queue.front()->value;
      }
      else
      {
          THROW_EXCEPTION(InvalidOperationException, "No value at current Node...");
        }
    }

四、通用樹結構的實現

1、通用樹節點的實現

 template <typename T>
  class GTreeNode:public TreeNode<T>
  {
  protected:
    bool m_flag;//堆空間標識
    //重載new操作符，聲明為保護
    void* operator new(unsigned int size)throw()
    {
      return Object::operator new(size);
    }
    GTreeNode(const GTreeNode<T>& other);
    GTreeNode<T>& operator = (const GTreeNode<T>& other);

  public:
    LinkedList<GTreeNode<T>*> m_children;
    GTreeNode()
    {
      //棧上分配的空間標識為false
      m_flag = false;
    }
    //工廠方法，創建堆空間的結點
    static GTreeNode<T>* NewNode()
    {
      GTreeNode<T>* ret = new GTreeNode<T>();
      if(ret != NULL)
      {
          //堆空間的結點標識為true
          ret->m_flag = true;
      }
      return ret;
    }
    //堆空間結點標識訪問函數
    bool flag()const
    {
      return m_flag;
    }
  };

2、通用樹的實現

 template <typename T>
  class GTree:public Tree<T>
  {
  protected:
    LinkedQueue<GTreeNode<T>*> m_queue;
    GTree(const GTree<T>& other);
    GTree<T>& operator=(const GTree<T>& other);
    GTreeNode<T>* find(GTreeNode<T>* node, const T& value)const
    {
      GTreeNode<T>* ret = NULL;
      if(node != NULL)
      {
          //如果根結點的就是目標結點
          if(node->value == value)
          {
              ret =  node;
          }
          else
          {
              //遍歷根節點的子結點
              for(node->m_children.move(0); !node->m_children.end() && (ret == NULL); node->m_children.next())
              {
                  //對每個子子結點進行查找
                  ret = find(node->m_children.current(), value);
              }
          }
      }
      return ret;
    }
    GTreeNode<T>* find(GTreeNode<T>* node, GTreeNode<T>* obj)const
    {
      GTreeNode<T>* ret = NULL;
      //根結點為目標結點
      if(node == obj)
      {
          ret =  node;
      }
      else
      {
          if(node != NULL)
          {
              //遍歷子結點
              for(node->m_children.move(0); !node->m_children.end() && (ret == NULL); node->m_children.next())
              {
                  ret = find(node->m_children.current(), obj);
              }
          }
      }
      return ret;
    }

    void free(GTreeNode<T>* node)
    {
      if(node != NULL)
      {
          for(node->m_children.move(0); !node->m_children.end(); node->m_children.next())
          {
              free(node->m_children.current());
          }
          //如果結點存儲在堆空間
          if(node->flag())
             delete node;//釋放
      }
    }

    void remove(GTreeNode<T>* node, GTree<T>*& ret)
    {
      ret = new GTree<T>();
      if(ret != NULL)
      {
          //如果刪除的結點是根結點
          if(root() == node)
          {
              this->m_root = NULL;
          }
          else
          {
              //獲取刪除結點的父結點的子結點鏈表
              LinkedList<GTreeNode<T>*>& child = dynamic_cast<GTreeNode<T>*>(node->parent)->m_children;
              //從鏈表中刪除結點
              child.remove(child.find(node));
              //結點的父結點置NULL
              node->parent = NULL;
          }
          //將刪除結點賦值給創建的樹ret的根結點
          ret->m_root = node;
      }
      else
      {
          THROW_EXCEPTION(NoEnoughMemoryException, "No enough memory...");
      }
    }

    int count(GTreeNode<T>* node) const
    {
      int ret = 0;
      if(node != NULL)
      {
          ret = 1;//根結點
          //遍歷根節點的子結點
          for(node->m_children.move(0); !node->m_children.end(); node->m_children.next())
          {
              ret += count(node->m_children.current());
          }
      }
      return ret;
    }

    int height(GTreeNode<T>* node)const
    {
      int ret = 0;
      if(node != NULL)
      {
          //遍歷子結點
          for(node->m_children.move(0); !node->m_children.end(); node->m_children.next())
          {
              //當前結點的高度
              int h = height(node->m_children.current());
              if(ret < h)
              {
                  ret = h;
              }
          }
          ret = ret + 1;
      }
      return ret;
    }

    int degree(GTreeNode<T>* node) const
    {
      int ret = 0;
      if(node != NULL)
      {
          //結點的子結點的數量
          ret = node->m_children.length();
          //遍歷子結點
          for(node->m_children.move(0); !node->m_children.end(); node->m_children.next())
          {
              int d = degree(node->m_children.current());
              if(ret < d)
              {
                  ret = d;
              }
          }
      }
      return ret;
    }
  public:
    GTree()
    {

    }
    //插入結點
    bool insert(TreeNode<T>* node)
    {
      bool ret = true;
      if(node != NULL)
      {
          //樹為空，插入結點為根結點
          if(this->m_root == NULL)
          {
              node->parent = NULL;
              this->m_root = node;
          }
          else
          {
              //找到插入結點的父結點
              GTreeNode<T>* np = find(node->parent);
              if(np != NULL)
              {
                  GTreeNode<T>* n = dynamic_cast<GTreeNode<T>*>(node);
                  //如果子結點中無該結點，插入結點
                  if(np->m_children.find(n) < 0)
                  {
                      ret = np->m_children.insert(n);
                  }
              }
              else
              {
                  THROW_EXCEPTION(InvalidOperationException, "Invalid node...");
              }
          }
      }
      else
      {
          THROW_EXCEPTION(InvalidParameterException, "Parameter is invalid...");
      }
      return ret;
    }
    bool insert(const T& value, TreeNode<T>* parent)
    {
      bool ret = true;
      GTreeNode<T>* node = GTreeNode<T>::NewNode();
      if(node != NULL)
      {
          node->value = value;
          node->parent = parent;
          insert(node);
      }
      else
      {
          THROW_EXCEPTION(NoEnoughMemoryException, "No enough memory...");
      }
      return ret;
    }
    //刪除結點
    SharedPointer<Tree<T>> remove(const T& value)
    {
      GTree<T>* ret = NULL;
      //找到結點
      GTreeNode<T>* node = find(value);
      if(node != NULL)
      {
          remove(node, ret);
          m_queue.clear();
      }
      else
      {
          THROW_EXCEPTION(InvalidParameterException, "Parameter invalid...");
      }
      return ret;
    }

    SharedPointer<Tree<T>> remove(TreeNode<T>* node)
    {
      GTree<T>* ret = NULL;
      node = find(node);
      if(node != NULL)
      {
          remove(dynamic_cast<GTreeNode<T>*>(node), ret);
          m_queue.clear();
      }
      else
      {
          THROW_EXCEPTION(InvalidParameterException, "Parameter invalid...");
      }
      return ret;
    }
    //查找結點
    GTreeNode<T>* find(const T& value)const
    {
      return find(root(), value);
    }
    GTreeNode<T>* find(TreeNode<T>* node)const
    {
        return find(root(), dynamic_cast<GTreeNode<T>*>(node));
    }
    //根結點訪問函數
    GTreeNode<T>* root()const
    {
        return dynamic_cast<GTreeNode<T>*>(this->m_root);
    }
    //樹的度訪問函數
    int degree()const
    {
        return degree(root());
    }
    //樹的高度訪問函數
    int height()const
    {
        height(root());
    }
    //樹的結點數目訪問函數
    int count()const
    {
        count(root());
    }
    //清空樹
    void clear()
    {
        free(root());
        this->m_root = NULL;
    }

    bool begin()
    {
      bool ret = (root() != NULL);
      if(ret)
      {
          //清空隊列
          m_queue.clear();
          //根節點加入隊列
          m_queue.add(root());
      }
      return ret;
    }

    bool end()
    {
        return (m_queue.length() == 0);
    }

    bool next()
    {
      bool ret = (m_queue.length() > 0);
      if(ret)
      {
          GTreeNode<T>* node = m_queue.front();
          m_queue.remove();//隊頭元素出隊
          //將隊頭元素的子結點入隊
          for(node->m_children.move(0); !node->m_children.end(); node->m_children.next())
          {
              m_queue.add(node->m_children.current());
          }
      }
      return ret;
    }

    T current()
    {
      if(!end())
      {
          return m_queue.front()->value;
      }
      else
      {
          THROW_EXCEPTION(InvalidOperationException, "No value at current Node...");
      }
    }
    virtual ~GTree()
    {
      clear();
    }
  };

分享題目：數據結構（十三）——樹
文章路徑：http://vcdvsql.cn/article4/iijjoe.html

成都網站建設公司_創新互聯，為您提供微信公眾號、服務器托管、云服務器、網站改版、外貿網站建設、定制開發

廣告

聲明：本網站發布的內容（圖片、視頻和文字）以用戶投稿、用戶轉載內容為主，如果涉及侵權請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網站立場，如需處理請聯系客服。電話：028-86922220；郵箱：631063699@qq.com。內容未經允許不得轉載，或轉載時需注明來源： 創新互聯