使用scikit-learn怎么實現線性回歸和多元回歸-創新互聯
使用scikit-learn怎么實現線性回歸和多元回歸?很多新手對此不是很清楚,為了幫助大家解決這個難題,下面小編將為大家詳細講解,有這方面需求的人可以來學習下,希望你能有所收獲。
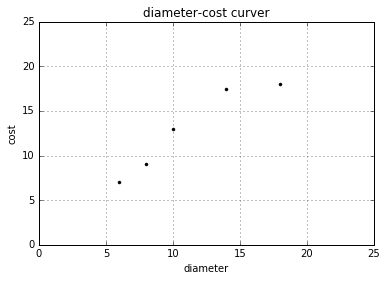
成都創新互聯服務項目包括商南網站建設、商南網站制作、商南網頁制作以及商南網絡營銷策劃等。多年來,我們專注于互聯網行業,利用自身積累的技術優勢、行業經驗、深度合作伙伴關系等,向廣大中小型企業、政府機構等提供互聯網行業的解決方案,商南網站推廣取得了明顯的社會效益與經濟效益。目前,我們服務的客戶以成都為中心已經輻射到商南省份的部分城市,未來相信會繼續擴大服務區域并繼續獲得客戶的支持與信任!匹薩的直徑與價格的數據
%matplotlib inline import matplotlib.pyplot as plt def runplt(): plt.figure() plt.title(u'diameter-cost curver') plt.xlabel(u'diameter') plt.ylabel(u'cost') plt.axis([0, 25, 0, 25]) plt.grid(True) return plt plt = runplt() X = [[6], [8], [10], [14], [18]] y = [[7], [9], [13], [17.5], [18]] plt.plot(X, y, 'k.') plt.show()
訓練模型
from sklearn.linear_model import LinearRegression
import numpy as np
# 創建并擬合模型
model = LinearRegression()
model.fit(X, y)
print('預測一張12英寸匹薩價格:$%.2f' % model.predict(np.array([12]).reshape(-1, 1))[0])預測一張12英寸匹薩價格:$13.68
一元線性回歸假設解釋變量和響應變量之間存在線性關系;這個線性模型所構成的空間是一個超平面(hyperplane)。
超平面是n維歐氏空間中余維度等于一的線性子空間,如平面中的直線、空間中的平面等,總比包含它的空間少一維。
在一元線性回歸中,一個維度是響應變量,另一個維度是解釋變量,總共兩維。因此,其超平面只有一維,就是一條線。
上述代碼中sklearn.linear_model.LinearRegression類是一個估計器(estimator)。估計器依據觀測值來預測結果。在scikit-learn里面,所有的估計器都帶有:
- fit()
- predict()
fit()用來分析模型參數,predict()是通過fit()算出的模型參數構成的模型,對解釋變量進行預測獲得的值。
因為所有的估計器都有這兩種方法,所有scikit-learn很容易實驗不同的模型。
一元線性回歸模型:
y=α+βx
一元線性回歸擬合模型的參數估計常用方法是:
- 普通最小二乘法(ordinary least squares )
- 線性最小二乘法(linear least squares)
首先,我們定義出擬合成本函數,然后對參數進行數理統計。
plt = runplt() plt.plot(X, y, 'k.') X2 = [[0], [10], [14], [25]] model = LinearRegression() model.fit(X, y) y2 = model.predict(X2) plt.plot(X, y, 'k.') plt.plot(X2, y2, 'g-') plt.show()
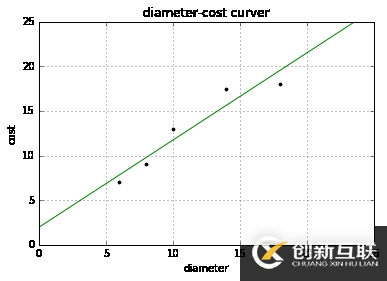
plt = runplt() plt.plot(X, y, 'k.') y3 = [14.25, 14.25, 14.25, 14.25] y4 = y2 * 0.5 + 5 model.fit(X[1:-1], y[1:-1]) y5 = model.predict(X2) plt.plot(X, y, 'k.') plt.plot(X2, y2, 'g-.') plt.plot(X2, y3, 'r-.') plt.plot(X2, y4, 'y-.') plt.plot(X2, y5, 'o-') plt.show()
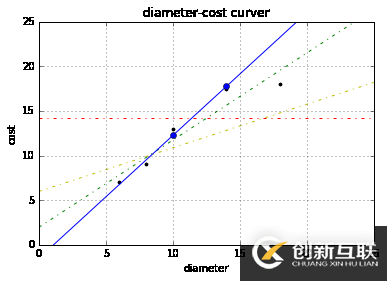
成本函數(cost function)也叫損失函數(loss function),用來定義模型與觀測值的誤差。模型預測的價格與訓練集數據的差異稱為殘差(residuals)或訓練誤差(training errors)。后面我們會用模型計算測試集,那時模型預測的價格與測試集數據的差異稱為預測誤差(prediction errors)或訓練誤差(test errors)。
模型的殘差是訓練樣本點與線性回歸模型的縱向距離,如下圖所示:
plt = runplt() plt.plot(X, y, 'k.') X2 = [[0], [10], [14], [25]] model = LinearRegression() model.fit(X, y) y2 = model.predict(X2) plt.plot(X, y, 'k.') plt.plot(X2, y2, 'g-') # 殘差預測值 yr = model.predict(X) for idx, x in enumerate(X): plt.plot([x, x], [y[idx], yr[idx]], 'r-') plt.show()
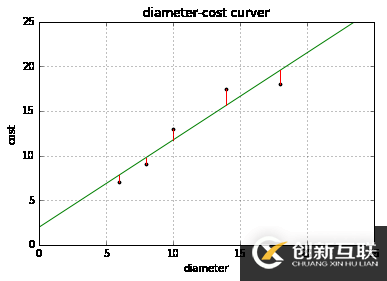
我們可以通過殘差之和最小化實現最佳擬合,也就是說模型預測的值與訓練集的數據最接近就是最佳擬合。對模型的擬合度進行評估的函數稱為殘差平方和(residual sum of squares)成本函數。就是讓所有訓練數據與模型的殘差的平方之和最小化,如下所示:
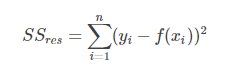
其中,
import numpy as np
print('殘差平方和: %.2f' % np.mean((model.predict(X) - y) ** 2))殘差平方和: 1.75
解一元線性回歸的最小二乘法
通過成本函數最小化獲得參數,我們先求相關系數 ββ 。按照頻率論的觀點,我們首先需要計算 xx 的方差和 xx 與 yy 的協方差。
方差是用來衡量樣本分散程度的。如果樣本全部相等,那么方差為0。方差越小,表示樣本越集中,反正則樣本越分散。方差計算公式如下:
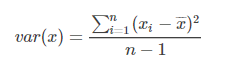
Numpy里面有var方法可以直接計算方差,ddof參數是貝塞爾(無偏估計)校正系數(Bessel's correction),設置為1,可得樣本方差無偏估計量。
print(np.var([6, 8, 10, 14, 18], ddof=1))
23.2
協方差表示兩個變量的總體的變化趨勢。如果兩個變量的變化趨勢一致,也就是說如果其中一個大于自身的期望值,另外一個也大于自身的期望值,那么兩個變量之間的協方差就是正值。 如果兩個變量的變化趨勢相反,即其中一個大于自身的期望值,另外一個卻小于自身的期望值,那么兩個變量之間的協方差就是負值。如果兩個變量不相關,則協方差為0,變量線性無關不表示一定沒有其他相關性。協方差公式如下:
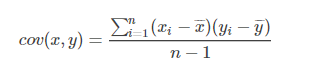
其中,
import numpy as np print(np.cov([6, 8, 10, 14, 18], [7, 9, 13, 17.5, 18])[0][1])
22.65
現在有了方差和協方差,就可以計算相關系統
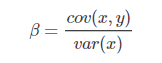
算出
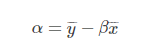
將前面的數據帶入公式就可以求出
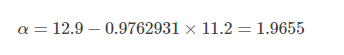
模型評估
前面我們用學習算法對訓練集進行估計,得出了模型的參數。有些度量方法可以用來評估預測效果,我們用R方(r-squared)評估匹薩價格預測的效果。R方也叫確定系數(coefficient of determination),表示模型對現實數據擬合的程度。計算R方的方法有幾種。一元線性回歸中R方等于皮爾遜積矩相關系數(Pearson product moment correlation coefficient或Pearson's r)的平方。種方法計算的R方一定介于0~1之間的正數。其他計算方法,包括scikit-learn中的方法,不是用皮爾遜積矩相關系數的平方計算的,因此當模型擬合效果很差的時候R方會是負值。下面我們用scikit-learn方法來計算R方。

R方是0.6620說明測試集里面過半數的價格都可以通過模型解釋。現在,讓我們用scikit-learn來驗證一下。LinearRegression的score方法可以計算R方:
# 測試集 X_test = [[8], [9], [11], [16], [12]] y_test = [[11], [8.5], [15], [18], [11]] model = LinearRegression() model.fit(X, y) model.score(X_test, y_test)
0.66200528638545164
多元回歸
from sklearn.linear_model import LinearRegression
X = [[6, 2], [8, 1], [10, 0], [14, 2], [18, 0]]
y = [[7], [9], [13], [17.5], [18]]
model = LinearRegression()
model.fit(X, y)
X_test = [[8, 2], [9, 0], [11, 2], [16, 2], [12, 0]]
y_test = [[11], [8.5], [15], [18], [11]]
predictions = model.predict(X_test)
for i, prediction in enumerate(predictions):
print('Predicted: %s, Target: %s' % (prediction, y_test[i]))
print('R-squared: %.2f' % model.score(X_test, y_test))Predicted: [ 10.06250019], Target: [11]
Predicted: [ 10.28125019], Target: [8.5]
Predicted: [ 13.09375019], Target: [15]
Predicted: [ 18.14583353], Target: [18]
Predicted: [ 13.31250019], Target: [11]
R-squared: 0.77
多項式回歸
上例中,我們假設解釋變量和響應變量的關系是線性的。真實情況未必如此。下面我們用多項式回歸,一種特殊的多元線性回歸方法,增加了指數項。現實世界中的曲線關系都是通過增加多項式實現的,其實現方式和多元線性回歸類似。本例還用一個解釋變量,匹薩直徑。讓我們用下面的數據對兩種模型做個比較:
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
X_train = [[6], [8], [10], [14], [18]]
y_train = [[7], [9], [13], [17.5], [18]]
X_test = [[6], [8], [11], [16]]
y_test = [[8], [12], [15], [18]]
# 建立線性回歸,并用訓練的模型繪圖
regressor = LinearRegression()
regressor.fit(X_train, y_train)
xx = np.linspace(0, 26, 100)
yy = regressor.predict(xx.reshape(xx.shape[0], 1))
plt = runplt()
plt.plot(X_train, y_train, 'k.')
plt.plot(xx, yy)
quadratic_featurizer = PolynomialFeatures(degree=2)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)
X_test_quadratic = quadratic_featurizer.transform(X_test)
regressor_quadratic = LinearRegression()
regressor_quadratic.fit(X_train_quadratic, y_train)
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_quadratic.predict(xx_quadratic), 'r-')
plt.show()
print(X_train)
print(X_train_quadratic)
print(X_test)
print(X_test_quadratic)
print('1 r-squared', regressor.score(X_test, y_test))
print('2 r-squared', regressor_quadratic.score(X_test_quadratic, y_test))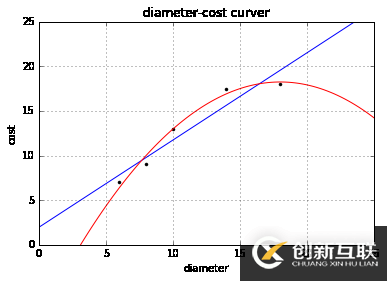
[[6], [8], [10], [14], [18]]
[[ 1. 6. 36.]
[ 1. 8. 64.]
[ 1. 10. 100.]
[ 1. 14. 196.]
[ 1. 18. 324.]]
[[6], [8], [11], [16]]
[[ 1. 6. 36.]
[ 1. 8. 64.]
[ 1. 11. 121.]
[ 1. 16. 256.]]
('1 r-squared', 0.80972683246686095)
('2 r-squared', 0.86754436563450732)plt = runplt()
plt.plot(X_train, y_train, 'k.')
quadratic_featurizer = PolynomialFeatures(degree=2)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)
X_test_quadratic = quadratic_featurizer.transform(X_test)
regressor_quadratic = LinearRegression()
regressor_quadratic.fit(X_train_quadratic, y_train)
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_quadratic.predict(xx_quadratic), 'r-')
cubic_featurizer = PolynomialFeatures(degree=3)
X_train_cubic = cubic_featurizer.fit_transform(X_train)
X_test_cubic = cubic_featurizer.transform(X_test)
regressor_cubic = LinearRegression()
regressor_cubic.fit(X_train_cubic, y_train)
xx_cubic = cubic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_cubic.predict(xx_cubic))
plt.show()
print(X_train_cubic)
print(X_test_cubic)
print('2 r-squared', regressor_quadratic.score(X_test_quadratic, y_test))
print('3 r-squared', regressor_cubic.score(X_test_cubic, y_test))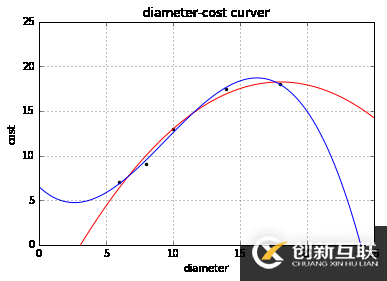
[[ 1.00000000e+00 6.00000000e+00 3.60000000e+01 2.16000000e+02]
[ 1.00000000e+00 8.00000000e+00 6.40000000e+01 5.12000000e+02]
[ 1.00000000e+00 1.00000000e+01 1.00000000e+02 1.00000000e+03]
[ 1.00000000e+00 1.40000000e+01 1.96000000e+02 2.74400000e+03]
[ 1.00000000e+00 1.80000000e+01 3.24000000e+02 5.83200000e+03]]
[[ 1.00000000e+00 6.00000000e+00 3.60000000e+01 2.16000000e+02]
[ 1.00000000e+00 8.00000000e+00 6.40000000e+01 5.12000000e+02]
[ 1.00000000e+00 1.10000000e+01 1.21000000e+02 1.33100000e+03]
[ 1.00000000e+00 1.60000000e+01 2.56000000e+02 4.09600000e+03]]
('2 r-squared', 0.86754436563450732)
('3 r-squared', 0.83569241560369567)plt = runplt()
plt.plot(X_train, y_train, 'k.')
quadratic_featurizer = PolynomialFeatures(degree=2)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)
X_test_quadratic = quadratic_featurizer.transform(X_test)
regressor_quadratic = LinearRegression()
regressor_quadratic.fit(X_train_quadratic, y_train)
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_quadratic.predict(xx_quadratic), 'r-')
seventh_featurizer = PolynomialFeatures(degree=7)
X_train_seventh = seventh_featurizer.fit_transform(X_train)
X_test_seventh = seventh_featurizer.transform(X_test)
regressor_seventh = LinearRegression()
regressor_seventh.fit(X_train_seventh, y_train)
xx_seventh = seventh_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_seventh.predict(xx_seventh))
plt.show()
print('2 r-squared', regressor_quadratic.score(X_test_quadratic, y_test))
print('7 r-squared', regressor_seventh.score(X_test_seventh, y_test))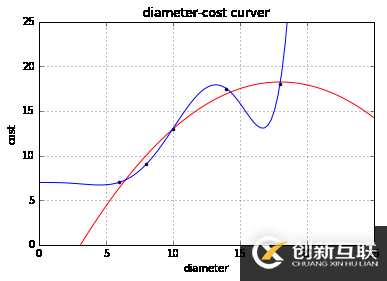
('2 r-squared', 0.86754436563450732)
('7 r-squared', 0.49198460568655)可以看出,七次擬合的R方值更低,雖然其圖形基本經過了所有的點。可以認為這是擬合過度(over-fitting)的情況。這種模型并沒有從輸入和輸出中推導出一般的規律,而是記憶訓練集的結果,這樣在測試集的測試效果就不好了。
正則化
LASSO方法會產生稀疏參數,大多數相關系數會變成0,模型只會保留一小部分特征。而嶺回歸還是會保留大多數盡可能小的相關系數。當兩個變量相關時,LASSO方法會讓其中一個變量的相關系數會變成0,而嶺回歸是將兩個系數同時縮小。
import numpy as np
from sklearn.datasets import load_boston
from sklearn.linear_model import SGDRegressor
from sklearn.cross_validation import cross_val_score
from sklearn.preprocessing import StandardScaler
from sklearn.cross_validation import train_test_split
data = load_boston()
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target)
X_scaler = StandardScaler()
y_scaler = StandardScaler()
X_train = X_scaler.fit_transform(X_train)
y_train = y_scaler.fit_transform(y_train.reshape(-1, 1))
X_test = X_scaler.transform(X_test)
y_test = y_scaler.transform(y_test.reshape(-1, 1))
regressor = SGDRegressor(loss='squared_loss',penalty="l1")
scores = cross_val_score(regressor, X_train, y_train.reshape(-1, 1), cv=5)
print('cv R', scores)
print('mean of cv R', np.mean(scores))
regressor.fit_transform(X_train, y_train)
print('Test set R', regressor.score(X_test, y_test))('cv R', array([ 0.74761441, 0.62036841, 0.6851797 , 0.63347999, 0.79476346]))
('mean of cv R', 0.69628119572104885)
('Test set R', 0.75084948718041566)
看完上述內容是否對您有幫助呢?如果還想對相關知識有進一步的了解或閱讀更多相關文章,請關注創新互聯成都網站設計公司行業資訊頻道,感謝您對創新互聯成都網站設計公司的支持。
另外有需要云服務器可以了解下創新互聯scvps.cn,海內外云服務器15元起步,三天無理由+7*72小時售后在線,公司持有idc許可證,提供“云服務器、裸金屬服務器、網站設計器、香港服務器、美國服務器、虛擬主機、免備案服務器”等云主機租用服務以及企業上云的綜合解決方案,具有“安全穩定、簡單易用、服務可用性高、性價比高”等特點與優勢,專為企業上云打造定制,能夠滿足用戶豐富、多元化的應用場景需求。
當前標題:使用scikit-learn怎么實現線性回歸和多元回歸-創新互聯
URL分享:http://vcdvsql.cn/article0/cessio.html
成都網站建設公司_創新互聯,為您提供關鍵詞優化、企業網站制作、域名注冊、自適應網站、網站改版、品牌網站設計
聲明:本網站發布的內容(圖片、視頻和文字)以用戶投稿、用戶轉載內容為主,如果涉及侵權請盡快告知,我們將會在第一時間刪除。文章觀點不代表本網站立場,如需處理請聯系客服。電話:028-86922220;郵箱:631063699@qq.com。內容未經允許不得轉載,或轉載時需注明來源: 創新互聯

- 當企業營銷型網站設計面包屑導航時,要切記哪些要點? 2022-08-06
- 網站建設中面包屑導航的使用 2022-11-17
- 面包屑導航優化 2022-02-14
- 成都網站推廣使用面包屑導航有什么優勢? 2022-09-26
- 網站建設中面包屑導航有哪些作用? 2022-10-01
- 網站建設中面包屑導航的作用? 2015-08-21
- 什么是面包屑導航和它的作用是什么 2021-09-21
- 淺談網站建設中的面包屑導航 2016-08-26
- 羅定網站建設為什么要做面包屑導航 2021-01-05
- 面包屑導航怎么做好SEO優化 2023-04-10
- 成都網站建設:面包屑導航的由來及其重要性! 2016-11-03
- 面包屑導航在網站建設中的作用是什么? 2023-01-11