數據結構-創新互聯

數據結構總目錄紅黑樹

介紹：
網站設計制作、網站設計的開發，更需要了解用戶，從用戶角度來建設網站，獲得較好的用戶體驗。創新互聯公司多年互聯網經驗，見的多，溝通容易、能幫助客戶提出的運營建議。作為成都一家網絡公司，打造的就是網站建設產品直銷的概念。選擇創新互聯公司，不只是建站，我們把建站作為產品，不斷的更新、完善，讓每位來訪用戶感受到浩方產品的價值服務。
紅黑樹是一種特化的AVL樹（平衡二叉樹），都是在進行插入和刪除操作時通過特定操作保持二叉查找樹的平衡，從而獲得較高的查找性能。
紅黑樹是一種平衡二叉查找樹的變體，它的左右子樹高差有可能大于 1，所以紅黑樹不是嚴格意義上的平衡二叉樹（AVL），但對之進行平衡的代價較低，其平均統計性能要強于 AVL
由于每一棵紅黑樹都是一顆二叉排序樹，因此，在對紅黑樹進行查找時，可以采用運用于普通二叉排序樹上的查找算法，在查找過程中不需要顏色信息

1. 圖文解析

紅黑樹性質

性質一：結點是紅色或黑色
性質二：根結點是黑色
性質三：空結點為葉子結點，且所有葉子結點都是黑色
性質四：每個紅色結點的兩個子結點都是黑色
性質五：從任一結點到其每個葉子的所有路徑都包含相同數目的黑色結點

1.1 存儲結構

與一般二叉樹相比，紅黑樹的結構存在父結點指針和結點顏色的標識

typedef char DataType;

typedef struct RBNode
{int color;                      // 結點顏色（0:黑色  1:紅色）
    DataType data;                  // 結點數據
    struct RBNode *parent;          // 父結點指針，用于定位
    struct RBNode *lchild, *rchild; // 左右孩子指針
}RBNode, *RBTree;

1.2 紅黑樹的插入操作

在紅黑樹的插入時，第一個問題就是新插入的結點應該為紅色還是黑色呢？
根據性質二：如果初始紅黑樹為空，則插入的一定是根節點且為黑色
根據性質五：如果新插入的結點為黑色，那么勢必會導致路徑上的黑色結點數量的增加，無疑增加了插入后的調整難度
根據性質三：如果新插入的結點為紅色，那么新結點的兩個空結點一定為黑色，那么就不會增加路徑上的黑色結點數量
總結：若插入的是根結點，則設置為黑色，其他情況則設置為紅色

已知新插入的結點為紅色，而如果父結點也為紅色，就會違反性質四，則說明此時需要調整紅黑樹
同時在父親結點為紅色的條件下，則根據性質二，父親結點一定不是根結點，且存在祖父結點

調整情況如下：

若父親結點為祖父結點的左孩子結點
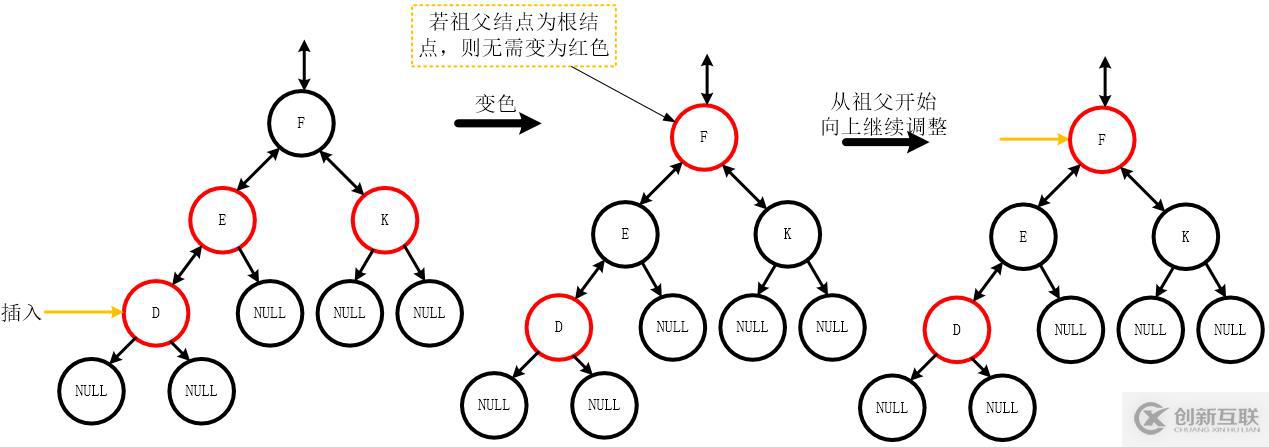
叔叔結點為紅色
調整過程：父親結點和叔叔結點均變為黑色，祖父結點若不是根結點，則變為紅色，并將祖父結點視為新插入的結點，繼續向上調整
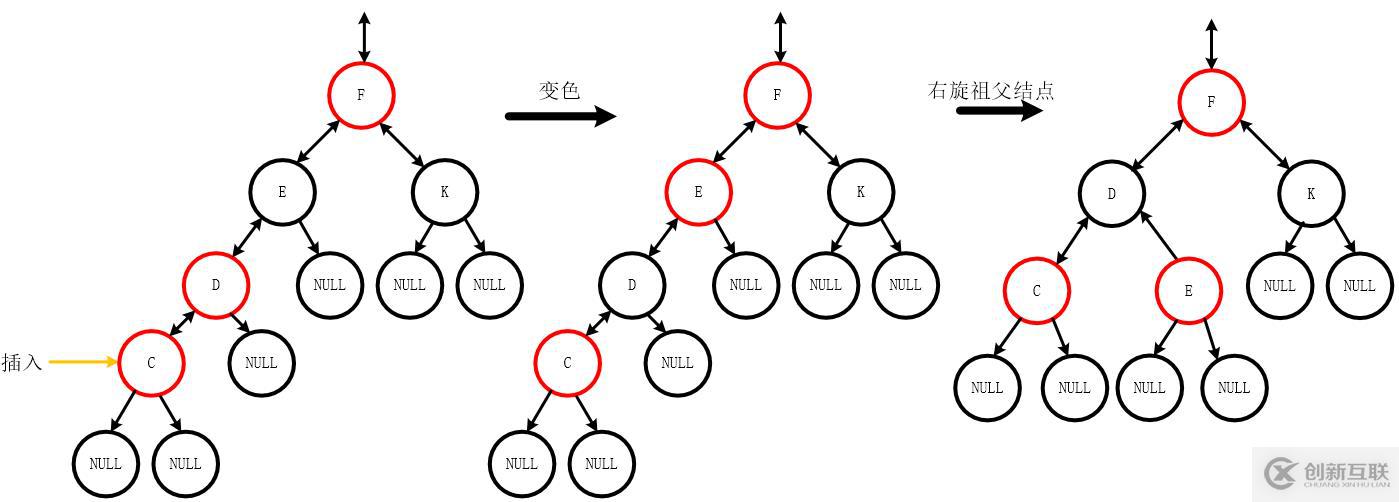
叔叔結點為黑色
2.1 插入的位置是父親結點的左孩子
調整過程：父親結點變為黑色，祖父結點變為紅色，最后右旋祖父結點
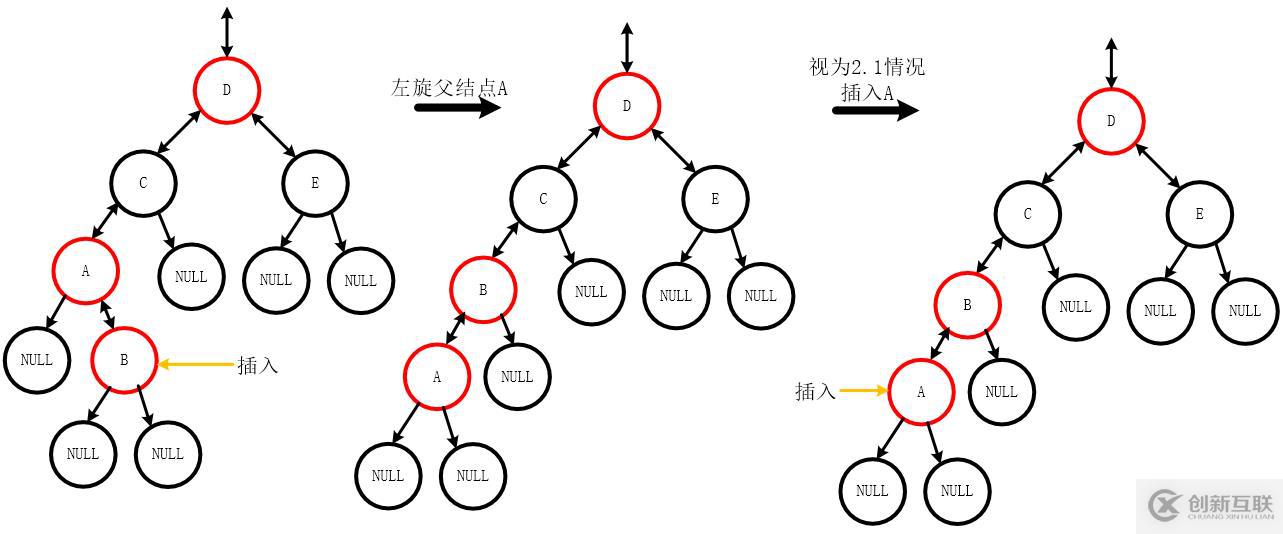
2.2 插入父親結點的右孩子
調整過程：左旋父結點，而后可視為2.1的情況進行調整
若父親結點為祖父結點的右孩子結點，其操作與以上情況對稱，詳細見代碼

2. 源代碼

#include#includetypedef char DataType;

typedef struct RBNode
{int color;                      // 結點顏色（0:黑色  1:紅色）
    DataType data;                  // 結點數據
    struct RBNode *parent;          // 父結點指針，用于定位
    struct RBNode *lchild, *rchild; // 左右孩子指針
}RBNode, *RBTree;

void InitRBTree(RBTree *T)
{(*T) = NULL;
    printf("紅黑樹已初始化!\n");
}

// 創建新結點
RBNode *NewNode(int color, DataType x)
{RBNode *newNode;
    newNode = (RBNode *)malloc(sizeof(RBNode));
    newNode->data = x;
    newNode->color = color;    
    newNode->parent = newNode->lchild = newNode->rchild = NULL;
    return newNode;
}

// 右旋轉， 
void RightRotate(RBNode *node, int flag)
{RBNode *parent = node->parent;
    RBNode *left = node->lchild;

    node->lchild = left->rchild;
    if (left->rchild)
    {left->rchild->parent = node;
    }
    
    left->rchild = node;
    node->parent = left;

    left->parent = parent;
    if (parent)
    {// flag = 0：node為父結點左孩子
        // flag = 1：node為父結點右孩子
        !flag ? (parent->lchild = left) : (parent->rchild = left);
    }
}

// 左旋轉
void LeftRotate(RBNode *node, int flag)
{RBNode *parent = node->parent;
    RBNode *right = node->rchild;
    
    node->rchild = right->lchild;
    if (right->lchild)
    {right->lchild->parent = node;
    }
    
    right->lchild = node;
    node->parent = right;

    right->parent = parent;
    if (parent)
    {// flag = 0：node為父結點左孩子
        // flag = 1：node為父結點右孩子
        !flag ? (parent->lchild = right) : (parent->rchild = right);
    }
}


// 紅黑樹調整
void RBTreeAdjust(RBNode *node)
{// 父結點為紅色，則父結點一定不是根結點，且祖父結點一定存在
    RBNode *father = node->parent;
    RBNode *grandfather = father->parent;
    RBNode *uncle;

    if (father && father == grandfather->lchild)
    {// 父親為祖父的左孩子
        uncle = grandfather->rchild;
        // printf("\t父親(%c)為祖父(%c)的左孩子\n", father->data, grandfather->data);
        if (uncle && uncle->color == 1)
        {// 若叔叔結點存在且為紅色，則進行變色
            // printf("\t\t叔叔(%c)為紅色，進行變色\n", uncle->data);
            father->color = 0;
            uncle->color = 0;
            grandfather->color = 1;
            // 遞歸調整祖父結點
            if (grandfather->parent && grandfather->parent->color == 1)
            {RBTreeAdjust(grandfather);
            }
            else if(!grandfather->parent)
            {grandfather->color = 0;
            }
        }
        // 叔叔結點不存在，或者為黑色
        else if (node == father->lchild)
        {// 若插入的結點是父親的左孩子，則進行變色并對祖父進行右旋轉
            // printf("\t\t叔叔為黑色，插入位置為父親的左孩子\n");
            // printf("\t\t>>父結點(%c)變黑色，祖父(%c)邊紅色, 右旋祖父\n", father->data, grandfather->data);

            father->color = 0;
            grandfather->color = 1;
            RightRotate(grandfather, 0);
        }
        else
        {// 若插入的結點是父親的右孩子，則對父親進行左旋轉
            // printf("\t\t叔叔為黑色，插入位置為父親的右孩子\n");
            // printf("\t\t>>左旋父親結點\n");
            
            LeftRotate(father, 0);
            RBTreeAdjust(father);
        }
    }
    else
    {// 父親為祖父的右孩子
        uncle = grandfather->lchild;
        // printf("\t父親(%c)為祖父(%c)的右孩子\n", father->data, grandfather->data);

        // 以下同理，對稱操作
        if (uncle && uncle->color == 1)
        {// printf("\t\t叔叔(%c)為紅色\n", uncle->data);
            father->color = 0;
            uncle->color = 0;
            grandfather->color = 1;
            // 遞歸調整祖父結點
            if (grandfather->parent && grandfather->parent->color == 1)
            {RBTreeAdjust(grandfather);
            }
            else  if(!grandfather->parent)
            {grandfather->color = 0;
            }
        }
        else if (node == father->lchild)
        {// printf("\t\t叔叔為黑色，插入位置為父親的左孩子\n");
            // printf("\t\t>>右旋父親結點\n");

            RightRotate(father, 1);
            RBTreeAdjust(father);
            
        }
        else
        {// printf("\t\t叔叔為黑色，插入位置為父親的右孩子\n");
            // printf("\t\t>>父結點(%c)變黑色，祖父(%c)邊紅色, 左旋祖父\n", father->data, grandfather->data);

            father->color = 0;
            grandfather->color = 1;
            LeftRotate(grandfather, 1);
        }
    }
}

// 插入
void RBTreeInsert(RBTree *T, DataType x)
{// 若樹為空，則創建新結點作為根結點
    if ((*T) == NULL)
    {// 性質二：根結點為黑色
        (*T) = NewNode(0, x);
        return;
    }

    // 根據二叉排序樹的性質查找插入位置
    RBNode *node = (*T), *parent;
    while (node)
    {parent = node;
        if (node->data >x)
        {node = node->lchild;
        }
        else if (node->data< x)
        {node = node->rchild;
        }
        else
        {printf("插入失敗，存在相同數據\n");
            return;
        }      
    }
    // 根據查找到的位置的父結點插入
    node = NewNode(1, x);
    if (parent->data >x)
    {parent->lchild = node;
    }
    else
    {parent->rchild = node;
    }
    node->parent = parent;
    
    
    // 若父結點為紅色，則不符合性質三：紅色結點的孩子結點均為黑色
    if (parent->color == 1)
    {// printf("父結點(%c)為紅色，需要進行調整!\n", parent->data);
        RBTreeAdjust(node);
    }
}



// 先序遍歷
void PreOrderTraverse(RBTree T)
{if (T)
    {printf("%c", T->data);
        T->color == 0 ? printf("[黑] ") : printf("[紅] ");
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);
    }
}


int main()
{RBTree T;
    DataType x;
    InitRBTree(&T);

    while (1)
    {fflush(stdin);
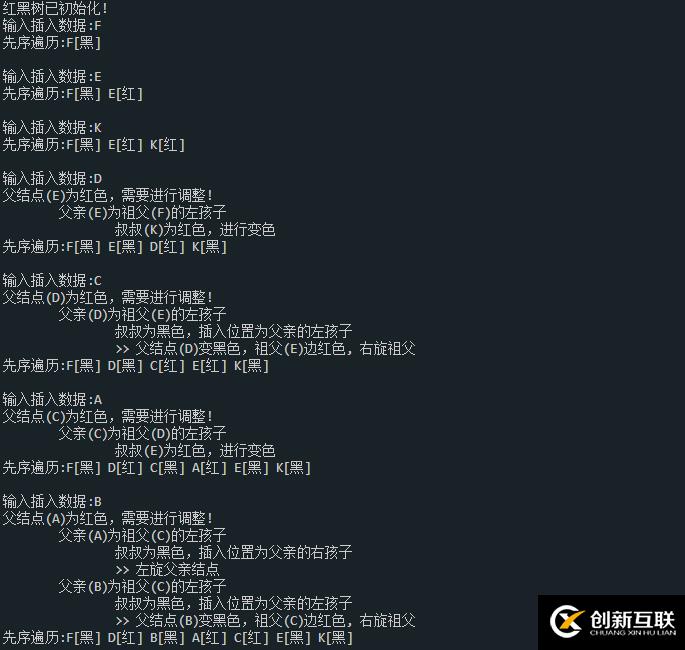
        printf("輸入插入數據:");    // 測試數據：FEKDCABNMOP
        scanf("%c", &x);
        if (x == '#')
        {break;
        }
        RBTreeInsert(&T, x);
        printf("先序遍歷:");
        PreOrderTraverse(T);
        printf("\n\n");
    }
    system("pause");
    return 0;
}