圖解代碼堆的構建及堆排序-創新互聯
- 堆的本質
- 堆的一般作用
- 建堆的主要思想及動圖解釋
- 堆中數據的刪除及動圖解釋
- 堆的存儲方式 及 父親和孩子節點的計算
- 堆的構建
- 堆的插入
- 堆的刪除
- 在無序數組上建堆(用數組中已有數據構建)
- 建堆時間復雜度
- 堆排序
- 堆排序的實現

堆的本質是完全二叉樹,但堆分為大堆和小堆
大堆:樹中所以的父親都大于左右孩子
小堆:樹中所有的父親都小于左右孩子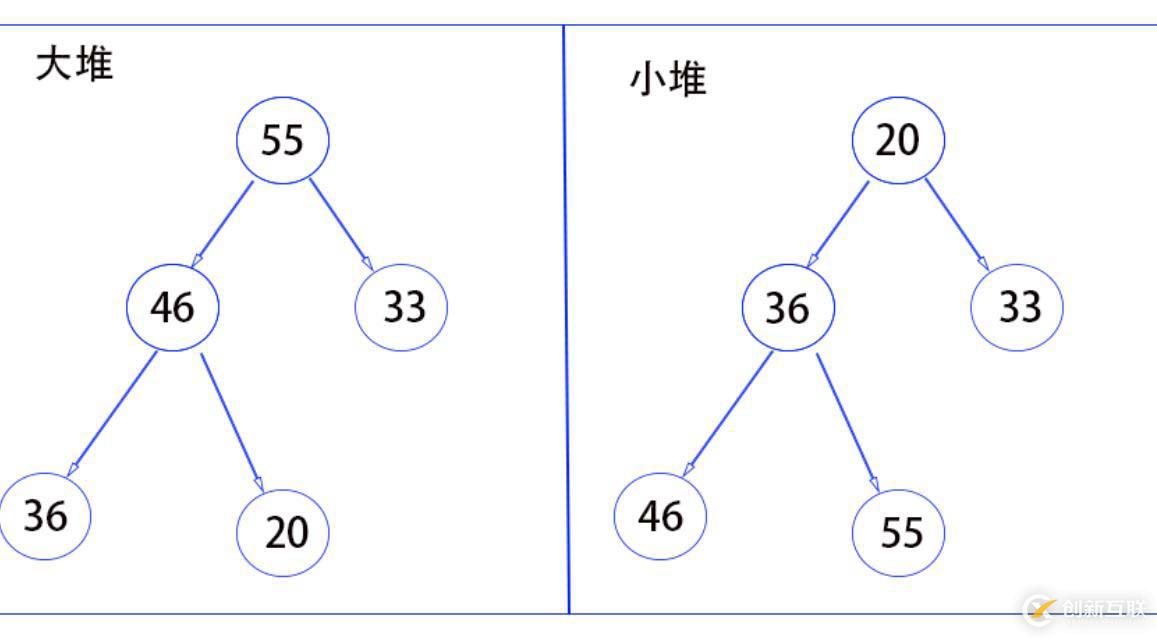
選出前n個大或最小的值,選大用大堆選小用小堆,以及堆排序的應用
但本文只涉及堆的建立及選出前n個大或最小的值
以大堆為列,從二叉樹下方插入數據(暫且稱為孩子)然后讓此孩子與父親節點比較如果他大于父親節點。則父親節點與與孩子節點交換位置,交換完后再與當前節點的父親節點比較如果仍比父親大則交換,如果小于等于則調整結束
這個調整過程由于是從二叉樹的下方向上比較并調整,所以咱可以把他稱為向上調整,如下圖是建大堆的過程建議觀看兩遍以上
上面已經說了堆一般都是用于解決前n個較大或較小的值,或者堆排序。所以堆中數據的刪除都是刪除堆頂,刪除中間的值意義不大但思想相同。所以這里主要講解如何刪除堆頂數據,以及刪除后如何調整。
總結:第一步將堆最后一位數據覆蓋到堆頂數據位置,然后與左右孩子中較大的一位比較,如比他小則交換位置。交換完后再與當前位置的左右孩子中較大的孩子比較,如比他小則交換位置。直至沒有孩子或比左右孩子都大為止。
這個調整過程由于是從二叉樹的上方向下方比較并調整,所以咱可以把他稱為向下調整
堆的存儲方式 及 父親和孩子節點的計算堆雖然是一顆完全二叉樹,但它的存儲方式一般為數組存儲,就是說堆的所有節點都存儲在數組當中。
如下圖
以下公式數據類型為int
孩子節點的計算
假設父節點的下標是parent,那么它的左孩子下標就是 2*parent+1;它的右孩子下標就是 2*parent+2 。
比如父親節點下標為 1 , 則其左孩子下標為 2 * 1 + 1 = 3 ;右孩子下標為 2 * 1 + 2 = 4(不懂對照圖多讀幾遍)
父親節點的計算
假設孩子節點下標為son(左右孩子均可),那他的父節下標(son-1)/2。
如孩子下標為4 ,則父親下標為 (4 - 1)/ 2 = 1;
比如插入一個10到數組的尾上,再進行向上調整算法,直到滿足堆的結構要求。
向上調整:從二叉樹下方插入數據(暫且稱為孩子)然后讓此孩子與父親節點比較如果他大于父親節點。則父親節點與與孩子節點交換位置,交換完后再與當前節點的父親節點比較如果仍比父親大則交換,如果小于等于則調整結束
刪除堆是刪除堆頂的數據,將堆頂的數據根最后一個數據一換,然后刪除數組最后一個數據,再進行向下調整算法。
向下調整:第一步將堆最后一位數據覆蓋到堆頂數據位置,然后與左右孩子中較大的一位比較,如比他小則交換位置。交換完后再與當前位置的左右孩子中較大的孩子比較,如比他小則交換位置。直至沒有孩子或比左右孩子都大為止。
下面是代碼實現功能包括:初始化,堆的銷毀,插入數據,刪除堆頂數據,查看堆頂數據,打印堆中數據等;
分三個源文件Heap.h是程序頭文件,heap.c是堆的功能性函數源文件,main.c是測試heap.c中函數功能用的
下面是heap.c
#include"Heap.h"
void HpInit(HP* head)//初始化
{assert(head);
head->data = NULL;
head->size = head->capacity = 0;
}
void HpDestroy(HP* head)//銷毀
{assert(head);
free(head->data);
head->data = NULL;
head->size = head->capacity = 0;
}
void Swp(HP* head, int sor, int parent)//交換函數
{HeapData cur = head->data[sor];
head->data[sor] = head->data[parent];
head->data[parent] = cur;
}
//插入調整函數
void Adjustup(HP* head)
{assert(head);
int sor = head->size;//要調整的數
while (sor >0)
{int parent = (sor - 1) / 2;//求其父親節點
if (head->data[sor]<= head->data[parent])
{ break;//比父親節點小或等于跳出
}
Swp(head, sor, parent);//如果比父親節點大就交換
sor = parent;
}
}
void HpPus(HP* head , HeapData data)//插入數據
{assert(head);//
if (head->capacity == head->size)//相等說明存滿了
{head->capacity == 0 ? (head->capacity = 4) : (head->capacity *= 2);
//head->capacity = 4;
HeapData* cur = (HeapData*)realloc(head->data, sizeof(HeapData) * head->capacity);
if (cur == NULL)//如果內存申請失敗
{ perror("realloc");
exit(-1);
}
head->data = cur;
}
//開始插入
head->data[head->size] = data;
//調整部分
Adjustup(head);
head->size++;//插入完成
}
void print(HP* head)//打印
{assert(head);
int i = 0;
while (i< head->size)
{printf("%d ", head->data[i]);
if ( i != 0 && i % 10 == 0 )
{ printf("\n");
}
i++;
}
}
//堆判空
bool HpEmpty(HP* head)
{assert(head);
return !head->size;//為空返回真
}
void AdjustDown(HP* head)//刪除后向下調整
{assert(head);
int parent = 0;
while (parent< head->size)
{int leftsor = parent * 2 + 1;//左孩子下標
if (leftsor >= head->size)//已經調整完成,沒有這個不會有bug,誤打誤撞對了而已
{ break;
}
if (leftsor + 1< head->size && head->data[leftsor]< head->data[leftsor + 1])
{ leftsor++;//找出左右孩子中較大的一位,注意leftsor + 1不要越界
}
if (head->data[parent] >= head->data[leftsor])//已經調整完成
{ break;
}
//如果parent小于他的孩子則交換
Swp(head, leftsor, parent);
parent = leftsor;
}
//調整完成結束
}
//堆的中間刪沒意義,一般都是刪除堆頂
void HpPop(HP* head)
{assert(head);
if (HpEmpty(head))
{printf("無數據\n");
return;
}
head->data[0] = head->data[head->size - 1];//刪除頭部數據
head->size--;
//向下調整數據
AdjustDown(head);
//刪除完成
}
HeapData HpTop(HP* head)//查看頭部數據
{assert(head);
if (HpEmpty(head))
{printf("無數據\n");
return -1;
}
return head->data[0];
}
int Hpsize(HP* head)//查看數據個數
{assert(head);
return head->size;
}下面是main.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
void Text1()
{HP head;
HpInit(&head);
int i = 0;
int x = 0;
do
{printf("\n1 插入 2 刪除 3 打印 4 查看頭部數據 \n");
printf("請輸入需要的功能\n");
scanf("%d", &i);
switch (i)
{case 1:
printf("請輸入數據\n");
scanf("%d", &x);
HpPus(&head, x);
break;
case 2:
HpPop(&head);
break;
case 3:
print(&head);
break;
case 4:
printf("%d", HpTop(&head));
break;
}
} while (i);
}
int main()
{Text1();
return 0;
}下面是Heap.h
#pragma once
#include#include#include#include
#includetypedef int HeapData;
typedef struct heap
{HeapData* data;
int size;//實際數據個數
int capacity;//空間容量
}HP;
void HpInit(HP* head);//初始化
void HpDestroy(HP* head);//銷毀
void HpPus(HP* head, HeapData data);//插入數據
void print(HP* head);//打印
void HpPop(HP* head);//頭刪
HeapData HpTop(HP* head);//查看頭部數據
int Hpsize(HP* head);//查看數據個數 下面我們給出一個數組,這個數組邏輯上可以看做一顆完全二叉樹,但是還不是一個堆,現在我們通過算法,把它構建成一個堆。根節點左右子樹不是堆,我們怎么調整呢?這里我們從倒數的第一個非葉子節點的子樹開始調整,一直調整到根節點的樹,就可以調整成堆。
下面是調整圖解,第一次調整的是最后一個數據的父親節點(假設孩子節點下標為son(左右孩子均可),那他的父節下標(son-1)/2。如孩子下標為4 ,則父親下標為 (4 - 1)/ 2 = 1;);
調整完后如最后一個數據的父親節點下標為,i ,則直接 i-- ,繼續將 i 下標視為堆頂繼續向下調整,直至i< 0 為止;
因為堆是完全二叉樹,而滿二叉樹也是完全二叉樹,此處為了簡化使用滿二叉樹來證明(時間復雜度本來看的就是近似值,多幾個節點不影響最終結果):
下面是代碼實現(為不破壞原有數組我是復制數組內容后再進行建堆的):
void AdjustDown(HeapData* arr,int parent, int size)
{int leftson = parent * 2 + 1;//左孩子
while (leftson< size)//
{if (leftson + 1< size && arr[leftson + 1] >arr[leftson])
{ leftson++;//如果右孩子大于左孩子
}
if (arr[leftson]< arr[parent])//如果孩子小于父親
{ break;
}
Sawp(arr, leftson, parent);
parent = leftson;
leftson = parent * 2 + 1;
}
}
void CreateHeap(HP* head, int* arr, int size)
{assert(head);
int parent, son = size - 1;
head->data = (HeapData*)malloc(sizeof(int) * size);//給數組的復制開辟空間
if (NULL == head->data)//如果開辟失敗
{perror("malloc");
exit(-1);
}
memcpy(head->data, arr, sizeof(int) * size);//拷貝需要建堆的數組
head->capacity = head->size = size;//開區間
for (parent = (son - 1) / 2; parent >= 0; parent--)//傳最后一個數字據的父親開始建堆
{AdjustDown(head->data, parent,head->size);//將父節點首地址傳過去
}
}堆排序即利用堆的思想來進行排序,總共分為兩個步驟:
- 建堆
升序:建大堆
降序:建小堆 - 利用堆刪除思想來進行排序
建堆和堆刪除中都用到了向下調整,因此掌握了向下調整,就可以完成堆序。
首先得用上面的的方法先建一個堆,再如下圖,先把堆頂數據與最后一位互換,交換結束再進行一次向下調整把換上來的數調整到合適的地方要滿足堆的結構要求。注意堆頂數據換到尾部后就不參與建堆了讓其保持不動
不斷的換,及調整直至堆只剩一個數
下面是代碼實現:
void Sawp(HeapData* arr, int x, int y)//交換函數
{HeapData ch = arr[x];
arr[x] = arr[y];
arr[y] = ch;
}
void AdjustDown(HeapData* arr,int parent, int size)//向下調整
{int leftson = parent * 2 + 1;//左孩子
while (leftson< size)//
{if (leftson + 1< size && arr[leftson + 1] >arr[leftson])
{ leftson++;//如果右孩子大于左孩子
}
if (arr[leftson]< arr[parent])//如果孩子小于父親
{ break;
}
Sawp(arr, leftson, parent);
parent = leftson;
leftson = parent * 2 + 1;
}
}
//堆排序
void HeapSort(int* arr, int size)
{assert(arr);
int parent, son = size - 1;
for (parent = (son - 1) / 2; parent >= 0; parent--)//傳最后一個數據的父親開始建堆
{AdjustDown(arr, parent, size);//將父節點首地址傳過去
}
//上面是建堆,下面需要進行堆排序
int Hpsize = size-1;//數組最后一位
for (Hpsize; Hpsize >0; Hpsize--)
{Sawp(arr, 0, Hpsize);//每次將較大值換到最后一位
AdjustDown(arr, 0 , Hpsize);//交換完后調整,不調整剛剛換的那一位
}
}到這就結束啦,不足的地方歡迎評論區指教
你是否還在尋找穩定的海外服務器提供商?創新互聯www.cdcxhl.cn海外機房具備T級流量清洗系統配攻擊溯源,準確流量調度確保服務器高可用性,企業級服務器適合批量采購,新人活動首月15元起,快前往官網查看詳情吧
標題名稱:圖解代碼堆的構建及堆排序-創新互聯
分享鏈接:http://vcdvsql.cn/article4/hchie.html
成都網站建設公司_創新互聯,為您提供網站營銷、用戶體驗、軟件開發、靜態網站、服務器托管、外貿網站建設
聲明:本網站發布的內容(圖片、視頻和文字)以用戶投稿、用戶轉載內容為主,如果涉及侵權請盡快告知,我們將會在第一時間刪除。文章觀點不代表本網站立場,如需處理請聯系客服。電話:028-86922220;郵箱:631063699@qq.com。內容未經允許不得轉載,或轉載時需注明來源: 創新互聯

- 網站設計APP設計如何傳達品牌感 2021-05-20
- Web版網站建設與APP設計之間的不同之處 2016-11-25
- app設計:如何處理加載頁面 2022-05-29
- APP設計中,圖標設計的這些點你get到了嗎? 2016-08-12
- 手機APP設計制作定律(二) 2016-11-04
- app設計技巧:國外大師教你四步設計框架 2022-05-29
- APP設計怎樣才能符合人體工程學? 2016-08-09
- 網頁設計和APP設計背景設計趨勢 2021-04-21
- APP設計的五大特性! 2022-11-15
- APP設計容易忽視的問題 2022-06-30
- APP設計|登錄注冊模塊詳解 2022-05-25
- 移動時代的APP設計應注意哪些問題? 2017-01-24